题目内容
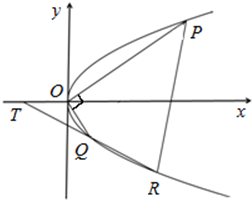 (2013•济南二模)设P(x1,y1),Q(x2,y2)是抛物线y2=2px(p>0)上相异两点,Q、P到y轴的距离的积为4且
(2013•济南二模)设P(x1,y1),Q(x2,y2)是抛物线y2=2px(p>0)上相异两点,Q、P到y轴的距离的积为4且| OP |
| OQ |
(1)求该抛物线的标准方程.
(2)过Q的直线与抛物线的另一交点为R,与x轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
分析:(1)由
•
=0,结合点P,Q在抛物线上,代入坐标后得到y1y2=-4p2,把纵坐标转化为横坐标后利用|x1x2|=4可求得p的值,则抛物线方程可求;
(2)连接PQ,PR分别叫x轴与点E,M,设出E和M的坐标,同时设出PQ,PR所在的直线方程,和抛物线方程联立后化为关于y的一元二次方程,利用根与系数的关系求出P,Q,R三点纵坐标的关系,再根据Q是T和R的中点找到E和M的坐标的关系,最终求出P和R纵坐标的乘积,用含有纵坐标的弦长公式写出弦PR长度,代入纵坐标的乘积后利用单调性求最小值.
| OP |
| OQ |
(2)连接PQ,PR分别叫x轴与点E,M,设出E和M的坐标,同时设出PQ,PR所在的直线方程,和抛物线方程联立后化为关于y的一元二次方程,利用根与系数的关系求出P,Q,R三点纵坐标的关系,再根据Q是T和R的中点找到E和M的坐标的关系,最终求出P和R纵坐标的乘积,用含有纵坐标的弦长公式写出弦PR长度,代入纵坐标的乘积后利用单调性求最小值.
解答:解:(1)∵
•
=0,则x1x2+y1y2=0,
又P、Q在抛物线上,故y12=2px1,y22=2px2,
故得
•
+y1y2=0,∴y1y2=-4p2,
∴|x1x2|=
=4p2,
又|x1x2|=4,故得4p2=4,p=1.
所以抛物线的方程为y2=2x;
(2)如图,设直线PQ过点E(a,0)且方程为x=my+a
联立方程组
,消去x得y2-2my-2a=0
∴
①
设直线PR与x轴交于点M(b,0),则可设直线PR方程为x=ny+b,并设R(x3,y3),
联立方程组
,消去x得y2-2ny-2b=0
∴
②
由①、②可得
=
由题意,Q为线段RT的中点,∴y3=2y2,∴b=2a.
又由(Ⅰ)知,y1y2=-4,代入①,可得
-2a=-4,∴a=2.故b=4.
∴y1y3=-8
∴|PR|=
|y1-y3|=
•
=2
•
≥4
.
当n=0,即直线PQ垂直于x轴时|PR|取最小值4
.
| OP |
| OQ |
又P、Q在抛物线上,故y12=2px1,y22=2px2,
故得
| y12 |
| 2p |
| y22 |
| 2p |
∴|x1x2|=
| (y1y2)2 |
| 4p2 |
又|x1x2|=4,故得4p2=4,p=1.

所以抛物线的方程为y2=2x;
(2)如图,设直线PQ过点E(a,0)且方程为x=my+a
联立方程组
|
∴
|
设直线PR与x轴交于点M(b,0),则可设直线PR方程为x=ny+b,并设R(x3,y3),
联立方程组
|
∴
|
由①、②可得
| y3 |
| y2 |
| b |
| a |
由题意,Q为线段RT的中点,∴y3=2y2,∴b=2a.
又由(Ⅰ)知,y1y2=-4,代入①,可得
-2a=-4,∴a=2.故b=4.
∴y1y3=-8
∴|PR|=
| 1+n2 |
| 1+n2 |
| (y1+y3)2-4y1y3 |
=2
| 1+n2 |
| n2+8 |
| 2 |
当n=0,即直线PQ垂直于x轴时|PR|取最小值4
| 2 |
点评:本题考查了抛物线的方程,考查了直线和圆锥曲线的关系,直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目