题目内容

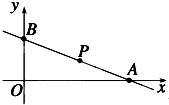
过定点P（2，1）作直线l，分别与x轴、y轴正向交于A，B两点，求使△AOB面积最小时的直线方程．
设所求的直线方程为
x
a
+
y
b
=1（a＞0，b＞0），由已知
2
a
+
1
b
=1．
于是
2
a
•
1
b
≤（
2
a
+
1
b
2
）2=
1
4
，当且仅当
2
a
=
1
b
=
1
2
，即a=4，b=2时，取最大值，
即S△AOB=
1
2
•ab取最小值4．
故所求的直线l的方程为
x
4
+
y
2
=1，即x+2y-4=0．
练习册系列答案
相关题目
已知直线l的方程为2x-3y-8=0．
（1）当直线l1过点A（-1，3），且l1∥l，求直线l1的方程；
（2）若点P（1，m）在直线l上，直线l2被两坐标轴截得的线段的中点恰为点P时，求直线l2的方程．
如图，矩形ABCD的两条对角线相交于点M（2，0），边AB所在直线的方程为x-3y-6=0，点T（-1，1）在边AD所在直线上．
（1）求边AD所在直线的方程；
（2）求点C的坐标；
（3）求矩形ABCD的面积．
已知直线l1：（a+2）x+（1-a）y-1=0与直线l2：（a-1）x+（2a+3）y+2=0垂直，则a=______．
已知直线l1：ax-y+b=0，l2：bx-y-a=0，则它们的图象可能为（　　）
A．B．C．D．
下列命题中正确的是（　　）
A．经过点P0（x0，y0）的直线都可以用方程y-y0=k（x-x0）表示
B．经过定点A（0，b）的直线都可以用方程y=kx+b表示
C．经过任意两个不同点P1（x1，y1），P2（x2，y2）的直线都可用方程（x2-x1）（y-y1）=（y2-y1）（x-x1）表示
D．不经过原点的直线都可以用方程
x
a
+
y
b
=1表示
如图，在平面直角坐标系xOy中，四边形OABC为平行四边形，其中O为坐标原点，且点B（4，4），C（1，3）．
（1）求线段AC中点坐标；
（2）过点C作CD垂直AB于点D，求直线CD的方程；
（3）求四边形OABC的面积．
已知直线l过点d（3，-4），且在两坐标轴上的截距相等，则l的方程为______．
对于平面直角坐标系内的任意两点A（x1，y1），B（x2，y2），A（x1，y1），B（x2，y2）定义它们之间的一种“距离”：||AB||=|x2-x1|+|y2-y1|．给出下列三个命题：
①若点C在线段AB上，则||AC||+||CB||=||AB||；
②在△ABC中，||AC||+||CB||＞||AB||；
③在△ABC中，若∠A=90°，则||AB||2+||AC||2=||BC||2．
其中错误的个数为（　　）
A．0B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网