Question

已知平面上的线段1及点P，任取1上的一点Q，线段PQ长度的最小值称为点P到线段1的距离，记为d（P，l）．设A（-3，1），B（0，1），C（-3，-1），D（2，-1），L₁=AB，L₂=CD，若P（x，y）满足d（P，L₁）=d（P，L₂），则y关于x的函数解析式为

y=

0 (x≤0) 1 4 x2 (0＜x≤2) x-1 (x＞2)

．

Answer 1

分析：该题就是寻找平面内到线段AB的距离等于到线段CD的距离相等的点的轨迹，当x≤0时，x轴上的点到线段AB的距离等于到线段CD的距离，当0＜x≤2时，点P到线段AB的距离即为到点B的距离，到点B的距离等于到直线CD的距离相等的点的轨迹为抛物线，当x＞2时，满足到线段AB的距离等于到线段CD的距离即为到点B与到点D的距离相等点，从而求出y关于x的函数解析式．

解答：解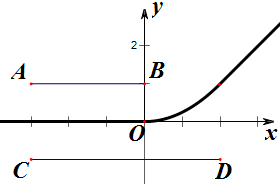：根据题意画出线段AB与线段CD，
∵P（x，y）满足d（P，L₁）=d（P，L₂），
∴点P满足到线段AB的距离等于到线段CD的距离，
当x≤0时，x轴上的点到线段AB的距离等于到线段CD的距离，故y=0（x≤0），
当0＜x≤2时，点P到线段AB的距离即为到点B的距离，到点B的距离等于到直线CD的距离相等的点的轨迹为抛物线，
根据抛物线的定义可知点B是抛物线的焦点，CD是准线，则

p

2

=1，
∴x²=4y，即y=

1

4

x²，（0＜x≤2），
当x＞2时，满足到线段AB的距离等于到线段CD的距离即为到点B与到点D的距离相等点，
在平面内到两定点距离相等的点即为线段BD的垂直平分线，
∴点P的轨迹为y=x-1（x＞2），
∴y关于x的函数解析式为：y=

0 (x≤0) 1 4 x2 (0＜x≤2) x-1 (x＞2)

．
故答案为：y=

0 (x≤0) 1 4 x2 (0＜x≤2) x-1 (x＞2)

．

点评：本题考查了分段函数的解析式的求法及其图象的作法，对于分段函数一般选用数形结合和分类讨论的数学思想进行解题．根据不同的范围研究不同的解析式，从而选定用分段函数来表示．属于中档题．