题目内容
已知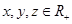 ,
,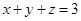 .
.
(1)求 的最小值;
的最小值;
(2)证明: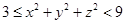 .
.
【答案】
(1)最小值为3;(2)证明过程详见解析.
【解析】
试题分析:本题主要考查利用基本不等式进行不等式的证明问题,考查学生的分析问题的能力和转化能力.第一问,用基本不等式分别对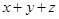 和
和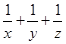 进行计算,利用不等式的可乘性,将两个式子乘在一起,得到所求的表达式的范围,注意等号成立的条件必须一致;第二问,先用基本不等式将
进行计算,利用不等式的可乘性,将两个式子乘在一起,得到所求的表达式的范围,注意等号成立的条件必须一致;第二问,先用基本不等式将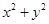 ,
, ,
, 变形,再把它们加在一起,得出已知中出现的
变形,再把它们加在一起,得出已知中出现的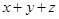 ,从而求出最小值,而所求证的式子的右边,须作差比较大小,只需证出差值小于0即可.
,从而求出最小值,而所求证的式子的右边,须作差比较大小,只需证出差值小于0即可.
试题解析:(Ⅰ)因为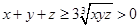 ,
, ,
,
所以 ,即
,即 ,
,
当且仅当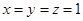 时,
时, 取最小值3. 5分
取最小值3. 5分
(Ⅱ)
 .
.
又 ,
,
所以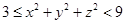 .
.
考点:1.基本不等式;2.不等式的性质;3.作差比较大小.

练习册系列答案
相关题目
 ,函数
,函数 .
. 的最值和单调递减区间;
的最值和单调递减区间;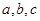 ,
, ,求△ABC的面积的最大值.
,求△ABC的面积的最大值. .
.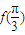 的值;
的值; ,求
,求 .
.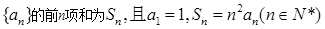 。
。 的值;
的值;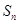 的表达式并用数学归纳法证明。
的表达式并用数学归纳法证明。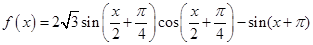 。
。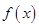 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 上的最大值和最小值。
上的最大值和最小值。