题目内容
昌九高速公路起于江西省南昌市蛟桥收费站,终于九江市荷花垄收费站,全长122Km,假设某汽车从九江荷花垄进入高速公路后以不低于60Km/小时,且不高于120Km/小时的速度匀速行驶到南昌蛟桥收费站,已知汽车每小时的运输成本y以元为单位)由固定部分和可变部分组成,固定部分为200元,可变部分与速度的平方成正比,当汽车以最快速度行驶时,每小时的运输成本为488元,若使汽车的全程 运输成本最低,其速度为( )km/小时.A.80
B.90
C.100
D.110
【答案】分析:因为每小时运输成本y(以元为单元)由可变部分和固定部分组成,固定部分是200,可变部分与速度v(千米/时)的平方成正比,根据每小时的运输成本为488元可求出比例系数为0.02,可求出可变部分为0.02v2,则求出汽车的全程运输成本y,最后利用基本不等式可求出所求.
解答:解:依题意得:y=200+kv2(60≤v≤120).
当v=120时,y=488=200+k•14400
∴k=0.02
∴汽车的全程运输成本y=(200+0.02v2)×
=122(0.02v+ )≥122×4=488(元)
)≥122×4=488(元)
当且仅当0.02v=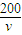 即v=100千米/时时取等号.
即v=100千米/时时取等号.
故选C.
点评:考查学生会根据题意列出函数关系,掌握基本不等式在最值问题中的应用注意等号成立的条件.
解答:解:依题意得:y=200+kv2(60≤v≤120).
当v=120时,y=488=200+k•14400
∴k=0.02
∴汽车的全程运输成本y=(200+0.02v2)×

=122(0.02v+
 )≥122×4=488(元)
)≥122×4=488(元)当且仅当0.02v=
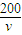 即v=100千米/时时取等号.
即v=100千米/时时取等号.故选C.
点评:考查学生会根据题意列出函数关系,掌握基本不等式在最值问题中的应用注意等号成立的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
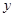 (以元为单位)由固定部分和可变部分组成,固定部分为200元,可变部分与速度的平方成正比,当汽车以最快速度行驶时,每小时的运输成本为488元,若使汽车的全程运输成本最低,其速度为( )km / 小时
(以元为单位)由固定部分和可变部分组成,固定部分为200元,可变部分与速度的平方成正比,当汽车以最快速度行驶时,每小时的运输成本为488元,若使汽车的全程运输成本最低,其速度为( )km / 小时