题目内容
（B题）已知圆C的方程为（x-1）2+y2=9，点p为圆上一动点，定点A（-1，0），线段AP的垂直平分线与直线CP交于点M，则为点M的轨迹为（ ）
分析：由题目给出的条件作出图形，结合线段垂直平分线上的点到线段两端点的距离相等及椭圆定义得到正确答案．
解答：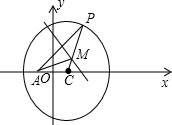
解：圆C：（x-1）2+y2=9，圆心为（1，0），半径为3，如图，
因为M是线段AP的垂直平分线与CP的交点，所以|MA|=|MP|，
所以|MA|+|MC|=|MC|+|MP|=|PC|=3．
而|AC|=2，|MA|+|MC|＞|AC|．
所以由椭圆定义知，M的轨迹是以A，C为焦点的椭圆．
故选A．
解：圆C：（x-1）2+y2=9，圆心为（1，0），半径为3，如图，因为M是线段AP的垂直平分线与CP的交点，所以|MA|=|MP|，
所以|MA|+|MC|=|MC|+|MP|=|PC|=3．
而|AC|=2，|MA|+|MC|＞|AC|．
所以由椭圆定义知，M的轨迹是以A，C为焦点的椭圆．
故选A．
点评：本题考查了椭圆的定义，考查了数学转化思想及数形结合的解题思想，是基础的定义题．
练习册系列答案
相关题目
如图，已知圆C的方程为：x2+y2-6x-8y+21=0，平面上有A（1，0）和B（-1，0）两点．
，求直线l的方程.
,求直线l的方程;
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求直线l的方程;
=(0,y0),若向量
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.