Question

师大附中高二某课题小组对长沙市工薪阶层对“楼市限购令”的态度进行调查，抽调了50人，他们月收入频数分布表及对“楼市限购令”赞成人数如下表：

月收入（百元	[15，25]	[25，35]	[35，45]	[45，55]	[55，65]	[65，75]
频数	5	10	15	10	5	5
赞成人数	4	8	12	5	3	1

（1）完成如图的月收入频率分布直方图，并估计被抽调人的月平均收入；
（2）若从月收入（单位：百元）在[15，25），[25，35）的被调查人中各随机选取两人进行追踪调查，记选中的4人中不赞成：“楼市限购令”的人数为ξ，求随机变量ξ的分布列和数学期望．

Answer 1

分析：（1）根据数据可得频率分布直方图，从而可估计被抽调人的月平均收入；
（2）ξ的可能取值有0，1，2，3，求出相应的概率，可得ξ的分布列及数学期望．

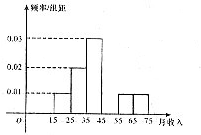
解答：解：（1）频率分布直方图如图所示

被抽调人的月平均收入为20××0.1+30×0.2+40×0.3+50×0.2+60×0.1+70×0.1=43百元；
（2）ξ的可能取值有0，1，2，3．
P（ξ=0）=

C 2 4

C 2 5

×

C 2 8

C 2 10

=

84

225

；P（ξ=1）=

C 1 4

C 2 5

×

C 2 8

C 2 10

+

C 2 4

C 2 5

×

C 1 8 C 1 2

C 2 10

=

104

225

；
P（ξ=2）=

C 1 4

C 2 5

×

C 1 8 C 1 2

C 2 10

+

C 2 4

C 2 5

×

C 2 2

C 2 10

=

35

225

；P（ξ=3）=

C 1 4

C 2 5

×

C 2 2

C 2 10

=

2

225

所以ξ的分布列是

ξ	0	1	2	3
P	84 225	104 225	35 225	2 225

所以ξ的期望值是Eξ=0×

84

225

+1×

104

225

+2×

35

225

+3×

2

225

=

4

5

．

点评：本题考查频率分布直方图，考查离散型随机变量的分布列与期望，考查学生的阅读与计算能力，属于中档题．