题目内容
有一隧道既是交通拥挤地段,又是事故多发地段.为了保证安全,交通部门规定,隧道内的车距d(m)正比于车速v(km/h)的平方与车身长l(m)的积,且车距不得小于一个车身长l(假设所有车身长均为l).而当车速为60(km/h)时,车距为1.44个车身长.
(1)求通过隧道的最低车速;
(2)在交通繁忙时,应规定怎样的车速,可以使隧道在单位时段内通过的汽车数量Q最多?
解:(1)根据题意得:d=kv2l,(d≥l),
当v=60,d=1.44l时,
代入解得:k=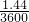 =0.0004,
=0.0004,
∵d≥l,∴0.0004v2l≥l
则v≥50,故最低车速为50km/h.
(2)因为两车间距为d,则两辆车头间的距离为l+d(m)
一小时内通过汽车的数量为Q最大,只需 最小,由(1)知Q=
最小,由(1)知Q=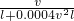 即Q=
即Q= ≤
≤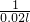
当 等号成立,即v=50km/h,Q取到最大值
等号成立,即v=50km/h,Q取到最大值
∴在交通繁忙时,应规定车速为50km/h,可以使隧道在单位时段内通过的汽车数量Q最多
分析:(1)根据已知条件即可列出一次函数关系式,先求出比例系数k后,根据d≥l建立不等关系,从而求出通过隧道的最低车速.
(2)因为两车间距为d,则两辆车头间的距离为l+d(m),则一小时内通过汽车的数量为Q= ,然后根据基本不等式可求出所求.
,然后根据基本不等式可求出所求.
点评:本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.
当v=60,d=1.44l时,
代入解得:k=
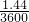 =0.0004,
=0.0004,∵d≥l,∴0.0004v2l≥l
则v≥50,故最低车速为50km/h.
(2)因为两车间距为d,则两辆车头间的距离为l+d(m)
一小时内通过汽车的数量为Q最大,只需
 最小,由(1)知Q=
最小,由(1)知Q=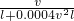 即Q=
即Q= ≤
≤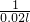
当
 等号成立,即v=50km/h,Q取到最大值
等号成立,即v=50km/h,Q取到最大值∴在交通繁忙时,应规定车速为50km/h,可以使隧道在单位时段内通过的汽车数量Q最多
分析:(1)根据已知条件即可列出一次函数关系式,先求出比例系数k后,根据d≥l建立不等关系,从而求出通过隧道的最低车速.
(2)因为两车间距为d,则两辆车头间的距离为l+d(m),则一小时内通过汽车的数量为Q=
 ,然后根据基本不等式可求出所求.
,然后根据基本不等式可求出所求.点评:本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
相关题目