题目内容
下列函数中,周期为1的奇函数是
- A.y=1-2sin2πx
- B.
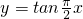
- C.y=sinπxcosπx
- D.
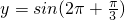
C
分析:将各项中的函数化简整理,对照三角函数的奇偶性和周期公式,即可得到只有C项符合题意.
解答:∵函数y=1-2sin2πx=cos2πx,满足f(-x)=f(x)
∴y=1-2sin2πx为偶函数,可得A项不正确;
因为函数y=tan x的周期为T=
x的周期为T=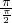 =2≠1,可得B项不正确.
=2≠1,可得B项不正确.
∵函数y=sinπxcosπx= sin2πx,满足f(-x)=-f(x)为奇函数,且T=
sin2πx,满足f(-x)=-f(x)为奇函数,且T=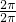 =1,
=1,
∴函数y=sinπxcosπx符合题意,得C项正确;
∵对于函数y=sin (2πx+ ),f(-x)=sin(-2πx+
),f(-x)=sin(-2πx+ )≠-sin(2πx+
)≠-sin(2πx+ ),
),
∴函数y=sin (2πx+ )不是奇函数,可得D项不正确.
)不是奇函数,可得D项不正确.
故选:C
点评:本题主要考查三角函数的奇偶性和最小正周期的求法,一般先将函数化简整理,再对照三角函数奇偶性和周期公式来解决.
分析:将各项中的函数化简整理,对照三角函数的奇偶性和周期公式,即可得到只有C项符合题意.
解答:∵函数y=1-2sin2πx=cos2πx,满足f(-x)=f(x)
∴y=1-2sin2πx为偶函数,可得A项不正确;
因为函数y=tan
 x的周期为T=
x的周期为T=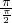 =2≠1,可得B项不正确.
=2≠1,可得B项不正确.∵函数y=sinπxcosπx=
 sin2πx,满足f(-x)=-f(x)为奇函数,且T=
sin2πx,满足f(-x)=-f(x)为奇函数,且T=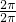 =1,
=1,∴函数y=sinπxcosπx符合题意,得C项正确;
∵对于函数y=sin (2πx+
 ),f(-x)=sin(-2πx+
),f(-x)=sin(-2πx+ )≠-sin(2πx+
)≠-sin(2πx+ ),
),∴函数y=sin (2πx+
 )不是奇函数,可得D项不正确.
)不是奇函数,可得D项不正确.故选:C
点评:本题主要考查三角函数的奇偶性和最小正周期的求法,一般先将函数化简整理,再对照三角函数奇偶性和周期公式来解决.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
下列函数中,周期为1的奇函数是( )
| A、y=1-2sin2πx | ||
B、y=sin (2πx+
| ||
C、y=tg
| ||
| D、y=sinπxcosπx |
下列函数中,周期为1的奇函数是( )
| A、y=sinπ|x| | ||
| B、y=|sinπx| | ||
| C、y=-sinπxcosπx | ||
D、y=
|
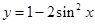 B
B
 D
D