题目内容
已知实数a、b满足log
a=log
b,下列五个关系式:
①a>b>1,②0<b<a<1,③b>a>1,④0<a<b<1,⑤a=b.其中不可能成立的关系式有( )个.
| 1 |
| 2 |
| 1 |
| 3 |
①a>b>1,②0<b<a<1,③b>a>1,④0<a<b<1,⑤a=b.其中不可能成立的关系式有( )个.
| A、1 | B、2 | C、3 | D、4 |
分析:在同一坐标系中画出函数y=log
x,y=log
x的图象,同函数图象分析可得当0<b<a<1时,或当b>a>1时,或当a=b=1时,足log
a=log
b,可能成立,进而即可得到答案.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:在同一坐标系中画出函数y=log
x,y=log
x的图象
如下图所示:
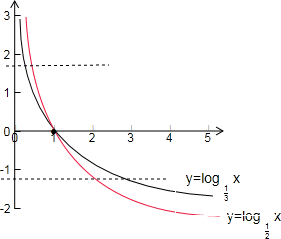
由图可得:当①a>b>1时log
a=log
b,不可能成立;
当④0<a<b<1时log
a=log
b,不可能成立;
故选B
| 1 |
| 2 |
| 1 |
| 3 |
如下图所示:

由图可得:当①a>b>1时log
| 1 |
| 2 |
| 1 |
| 3 |
当④0<a<b<1时log
| 1 |
| 2 |
| 1 |
| 3 |
故选B
点评:本题考查的知识点是对数函数的单调性与特殊点,画出满足条件的函数图象,然后利用数形结合的思想解答本题的关键是根据对数函数底数与函数图象形状及位置的关系,准确画出函数的图象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
(2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答, =a+bi,则过坐标原点和点A(a,b)的直线l的斜率为( )
=a+bi,则过坐标原点和点A(a,b)的直线l的斜率为( )


