题目内容
已知m∈R,设P:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立.Q:函数f(x)=x3+mx2+(m+| 4 | 3 |
分析:由题设知x1+x2=a且x1+x2=-2,所以,|x1-x2|=
=
≤3,由题意,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[1,1]恒成立的m的解集等于不等式|m2-5m-3|≥3的解集,由此知当m≤1或0≤m≤5或m≥6时,P是正确的.f′(x)=3x2+2mx+m+
,由题设能够得到当且仅当△>0时,函数f(x)在(-∞,+∞)上有极值.
由△=4m2-12m-16>0得m<1或m>4时,Q是正确得.由此可知使P正确且Q正确时,求出实数m的取值范围.
| (x1+x2)2-4x1x2 |
| a2+8 |
| 4 |
| 3 |
由△=4m2-12m-16>0得m<1或m>4时,Q是正确得.由此可知使P正确且Q正确时,求出实数m的取值范围.
解答:解:由题设x1和x2是方程x2-ax-2=0的两个实根,得x1+x2=a且x1x2=-2,
所以,|x1-x2|=
=
当a∈[-1,1]时,a2+8的最大值为9,即|x1-x2|≤3
由题意,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[1,1]恒成立的m的解集等于不等式|m2-5m-3|≥3的解集,由此不等式得m2-5m-3≤-3①
或m2-5m-3≥3②
不等式①的解为0≤m≤5不等式②的解为m≤1或m≥6因为,对m≤1或0≤m≤5或m≥6时,P是正确的.
对函数f(x)=x3+mx2+(m+
)x+6求导f′(x)=3x2+2mx+m+
令f'(x)=0,即3x2+2mx+m+
=0此一元二次不等式的判别式△=4m2-12(m+
)=4m2-12m-16.
若△=0,则f'(x)=0有两个相等的实根x0,且f'(x)的符号如下:
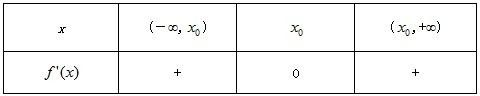
因此,f(x0)不是函数f(x)的极值.
若△>0,则f'(x)=0有两个不相等的实根x1和x2(x1<x2),且f'(x)的符号如下:

因此,函数f(x)在x=x1处取得极大值,在x=x2处取得极小值.
综上所述,当且仅当△>0时,函数f(x)在(-∞,+∞)上有极值.
由△=4m2-12m-16>0得m<-1或m>4,
因为,当m<1或m>4时,Q是正确的.
综上,使P正确且Q正确时,实数m的取值范围为(-∞,-1)∪(4,5]∪[6,+∞).
所以,|x1-x2|=
| (x1+x2)2-4x1x2 |
| a2+8 |
当a∈[-1,1]时,a2+8的最大值为9,即|x1-x2|≤3
由题意,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[1,1]恒成立的m的解集等于不等式|m2-5m-3|≥3的解集,由此不等式得m2-5m-3≤-3①
或m2-5m-3≥3②
不等式①的解为0≤m≤5不等式②的解为m≤1或m≥6因为,对m≤1或0≤m≤5或m≥6时,P是正确的.
对函数f(x)=x3+mx2+(m+
| 4 |
| 3 |
| 4 |
| 3 |
令f'(x)=0,即3x2+2mx+m+
| 4 |
| 3 |
| 4 |
| 3 |
若△=0,则f'(x)=0有两个相等的实根x0,且f'(x)的符号如下:

因此,f(x0)不是函数f(x)的极值.
若△>0,则f'(x)=0有两个不相等的实根x1和x2(x1<x2),且f'(x)的符号如下:

因此,函数f(x)在x=x1处取得极大值,在x=x2处取得极小值.
综上所述,当且仅当△>0时,函数f(x)在(-∞,+∞)上有极值.
由△=4m2-12m-16>0得m<-1或m>4,
因为,当m<1或m>4时,Q是正确的.
综上,使P正确且Q正确时,实数m的取值范围为(-∞,-1)∪(4,5]∪[6,+∞).
点评:本题考查命题真假的判断的应用,难度较大,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有两个不同的零点.求使“P且Q”为真命题的实数m的取值范围.
有两个不同的零点.求使“P且Q”为真命题的实数m的取值范围.