题目内容

已知m∈R，设P：不等式m2+16≤10m；Q：函数f（x）=3x2+2mx+m+
43
有两个不同的零点，求使“P∧Q”为真命题的实数m的取值范围．
分析：若使“P∧Q”为真命题，则P，Q都是真命题，则只要分别求出P，Q所对应的m的范围，即可求解
解答：解：∵m2+16≤10m
∴m2-10m+16≤0，解不等式可得，2≤m≤8
∴P：2≤m≤8
∵函数f（x）=3x2+2mx+m+
4
3
有两个不同的零点，
∴△=4m2-12(m+
4
3
)＞0
解不等式可得，m＞4或m＜-1
即Q：m＞4或m＜-1
若使“P∧Q”为真命题，则P，Q都是真命题
∴
2≤m≤8
m＞4或m＜-1

∴实数m的取值范围是4＜m≤8
点评：本题主要考查了P且Q复合命题的真假关系的应用，解题的关键是利用不等式及函数的知识求解出M，Q都为真命题的范围
练习册系列答案
相关题目
已知函数f（x）=lnx，g(x)=
12
ax2+bx(a≠0)
（1）若a=-2时，h（x）=f（x）-g（x）在其定义域内单调递增，求b的取值范围；
（2）设函数f（x）的图象C1与函数g（x）的图象C2交于P，Q两点，过线段PQ的中点R作x轴的垂线分别交C1、C2于点M，N，问是否存在点R，使C1在M处的切线与C2在N处的切线平行？若存在，求R的横坐标，若不存在，请说明理由．
已知A、B分别是直线y=
3
3
x和y=-
3
3
x上的两个动点，线段AB的长为2
3
，P是AB的中点．
（1）求动点P的轨迹C的方程；
（2）过点Q（1，0）任意作直线l（与x轴不垂直），设l与（1）中轨迹C交于M、N，与y轴交于R点．若
RM
=λ
MQ
，
RN
=μ
NQ
，证明：λ+μ 为定值．
已知h（x）是指数函数，且过点（ln2，2），令f（x）=h（x）+ax．
（I）求f（x）的单调区间；
（II）记不等式h（x）＜（1-a）x的解集为P，若M={x|
12
≤x≤2}且M∪P=P，求实数a的取值范围；
（III）当a=-1时，设g（x）=h（x）lnx，问是否存在x0∈（0，+∞），使曲线C：y=g（x）-f（x）在点x0处的切线斜率与f（x）在R上的最小值相等？若存在，求出符合条件的x0的个数；若不存在，请说明理由．
已知m∈R，设p：复数z1=（m-1）+（m+3）i （i是虚数单位）在复平面内对应的点在第二象限，q：复数z2=1+（m-2）i的模不超过
10
．
（1）当p为真命题时，求m的取值范围；
（2）若命题“p且q”为假命题，“p或q”为真命题，求m的取值范围．
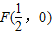已知点，动圆P经过点F，与直线x=-相切，设动圆的圆心P的轨迹为曲线W，且直线x-y=m与曲线W相交于A（x1，y1），B（x2，y2）两点，O为坐标原点．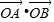
（1）求曲线W的方程；
（2）当m=2时，证明：OA⊥OB；
（3）当y1y2=-2m时，是否存在m∈R，使得=-1？若存在，求出m的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网