题目内容
(10分) 已知圆 :
: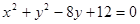 ,和定点
,和定点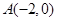 ,
,
求:(1) 过点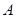 作圆
作圆 的切线
的切线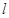 ,求直线
,求直线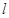 方程;
方程;
(2)
过点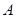 作直线
作直线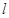 与圆
与圆 相交于
相交于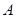 、
、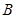 两点,且
两点,且 时,求直线
时,求直线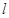 的方程.
的方程.
【答案】
(1) x=-2和3x-4y+6=0 (2) y=7x+14和y=x+2 。
【解析】本试题主要是考查了线圆相切的问题,求解直线的方程的运用。以及直线与圆相交的弦长公式的运用。
(1)因为将圆C的方程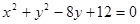 配方得标准方程为
配方得标准方程为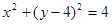 ,
,
则此圆的圆心为(0 , 4),半径为2.根据圆心到直线的距离可知斜率的值。注意对k的讨论是否存在的运用。
(2)若直线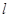 的斜率不存在不合题意;设直线
的斜率不存在不合题意;设直线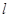 的方程为y=k(x+2),
的方程为y=k(x+2),
过圆心C作CD⊥AB,则根据题意和圆的性质,关于k的关系式得到求解。
解:将圆C的方程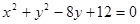 配方得标准方程为
配方得标准方程为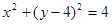 ,
,
则此圆的圆心为(0 , 4),半径为2.
(1)若直线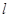 的斜率不存在时,容易验证直线x=-2,为切线;
的斜率不存在时,容易验证直线x=-2,为切线;
若直线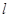 的斜率存在时,设直线
的斜率存在时,设直线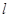 的方程为y=k(x+2), 与圆C相切,则有
的方程为y=k(x+2), 与圆C相切,则有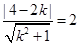 .
.
解得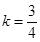 ,直线
,直线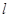 的方程为y=
的方程为y=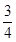 (x+2),即3x-4y+6=0
(x+2),即3x-4y+6=0
综上所求直线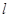 方程为x=-2和3x-4y+6=0
方程为x=-2和3x-4y+6=0
(2)若直线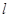 的斜率不存在不合题意;设直线
的斜率不存在不合题意;设直线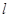 的方程为y=k(x+2),
的方程为y=k(x+2),
过圆心C作CD⊥AB,则根据题意和圆的性质,得

解得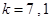 ,从而得所求直线方程为y=7x+14和y=x+2
,从而得所求直线方程为y=7x+14和y=x+2

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
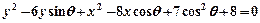 。
。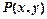 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求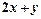 的取值范围。
的取值范围。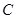 经过
经过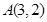 、
、 两点,且圆心在直线
两点,且圆心在直线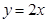 上.
上.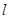 经过点
经过点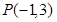 且与圆
且与圆 以
以 为圆心且经过原点O,与
为圆心且经过原点O,与 轴交于另一点A,与
轴交于另一点A,与 轴交于另一点B.
轴交于另一点B. 为定值
为定值 与圆
与圆 ,若
,若 ,求圆
,求圆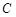 的方程.
的方程. :
:
 与圆C相交于A、B两点,求实数
与圆C相交于A、B两点,求实数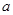 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 ,
若存在,求出实数
,
若存在,求出实数