题目内容
 21、 选修1:几何证明选讲
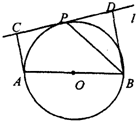
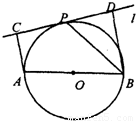
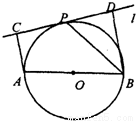
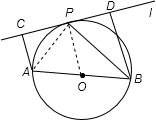
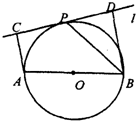
21、 选修1:几何证明选讲如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
分析:(1)连接OP,由AC与BD都与直线l垂直,得到AC与BD平行,由AB与l不相交得到四边形ABDC为梯形,又O为AB中点,P为CD中点,所以OP为梯形的中位线,根据梯形中位线性质得到OP与BD平行,从而得到OP与l垂直,而P在圆上,故l为圆的切线;
(2)由(1)得到l为圆的切线,根据弦切角等于夹弧所对的圆周角得到∠BPD=∠BAP,又根据等角的余角相等即可得到∠PBA=∠PBD,即PB为角平分线.
(2)由(1)得到l为圆的切线,根据弦切角等于夹弧所对的圆周角得到∠BPD=∠BAP,又根据等角的余角相等即可得到∠PBA=∠PBD,即PB为角平分线.
解答:证明:(1)连接OP,因为AC⊥l,BD⊥l,
所以AC∥BD.
又OA=OB,PC=PD,
所以OP∥BD,从而OP⊥l.
因为P在⊙O上,所以l是⊙O的切线.
(2)连接AP,因为l是⊙O的切线,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,即PB平分∠ABD.
所以AC∥BD.
又OA=OB,PC=PD,
所以OP∥BD,从而OP⊥l.
因为P在⊙O上,所以l是⊙O的切线.
(2)连接AP,因为l是⊙O的切线,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,即PB平分∠ABD.

点评:此题考查了切线的判定,梯形中位线性质及直线与圆的位置关系.证明切线时:有点连接圆心与这点,证明垂直;无点作垂线,证明垂线段等于圆的半径,是经常连接的辅助线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 选修1:几何证明选讲
选修1:几何证明选讲