题目内容
已知函数 .
.
(Ⅰ)求函数 在
在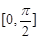 上的值域;
上的值域;
(Ⅱ)若对于任意的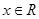 ,不等式
,不等式 恒成立,求
恒成立,求 .
.
【答案】
(Ⅰ)[-3,3];(Ⅱ)
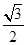 .
.
【解析】
试题分析:(Ⅰ)先利用三角恒等变换公式化简,再求在定义域范围上的值域;(Ⅱ)根据不等式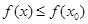 恒成立,得
恒成立,得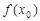 是
是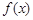 的最大值,从而得
的最大值,从而得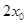 的范围,最后求
的范围,最后求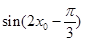 的值.
的值.
试题解析:
解:(Ⅰ)
 ,3分
,3分
∵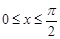 ,∴
,∴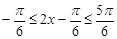 ,∴
,∴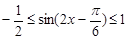 ,
,
∴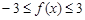 ,即函数
,即函数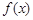 在
在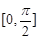 上的值域是[-3,3].
6分
上的值域是[-3,3].
6分
(Ⅱ)∵对于任意的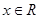 ,不等式
,不等式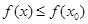 恒成立,
恒成立,
∴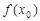 是
是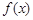 的最大值,∴由
的最大值,∴由 ,解得
,解得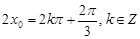 ,10分
,10分
∴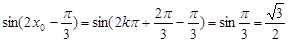 .
12分
.
12分
考点:1、二倍角公式;2、三角恒等变换;3、三角函数的值域;4、三角函数的基本运算.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.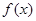 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求