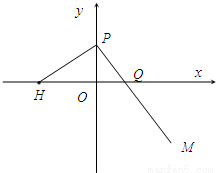
题目内容
点H(-3,0),点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且满足| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
(1)当点P在y轴上移动时,求点M的轨迹C的方程
(2)过定点D(m,0)(m>0)做直线l交轨迹C于A、B两点,E是D关于坐标原点的对称点,求证:∠AED=∠BED.
(3)在(2)中,是否存在垂直于x轴的直线被以AD为直径的圆截得的弦长恒为定值?若存在,求出直线的方程,若不存在,说明理由.
分析:(1)设M(x,y),则P(0,-
),Q(
,0)则可得,
=(3,-
),
=(x,
),由
•
=0代入整理可求
(2)要证明∠AED=∠BED,根据直线的倾斜角与斜率的关系,只要证KAE=-KBE即可
(3)假设存在满足条件的直线,根据垂径定理得性质可知,要使正弦长为定值,则只要圆心到直线的距离为定值即可
| y |
| 2 |
| x |
| 3 |
| HP |
| y |
| 2 |
| PM |
| 3y |
| 2 |
| HP |
| PM |
(2)要证明∠AED=∠BED,根据直线的倾斜角与斜率的关系,只要证KAE=-KBE即可
(3)假设存在满足条件的直线,根据垂径定理得性质可知,要使正弦长为定值,则只要圆心到直线的距离为定值即可
解答:解:(1)设M(x,y),则P(0,-
),Q(
,0)
则可得,
=(3,-
),
=(x,
)
∴
•
=3x-
=0
所以:y2=4x
(2)当AB垂直x轴时,A、B关于x轴对称,所以∠AED=∠BED
当AB存在斜率时,设直线AB:y=k(x-m),A(x1,y1),B(x2,y2)
kAE+kBE=
+
=
=0
所以kAE=-kBE
所以∠AED=∠BED
(3)假设存在垂直x轴的直线x=n,弦长为d
则
当m=1时不存在
当m>0且m≠1时,存在直线x=m-1
| y |
| 2 |
| x |
| 3 |
则可得,
| HP |
| y |
| 2 |
| PM |
| 3y |
| 2 |
∴
| HP |
| PM |
| 3y2 |
| 4 |
所以:y2=4x
(2)当AB垂直x轴时,A、B关于x轴对称,所以∠AED=∠BED
当AB存在斜率时,设直线AB:y=k(x-m),A(x1,y1),B(x2,y2)
|
kAE+kBE=
| y1 |
| x1+m |
| y2 |
| x2+m |
| k(x1-m)(x2+m)+k(x2-m)(x1+m) |
| (x1+m)(x2+m) |
所以kAE=-kBE
所以∠AED=∠BED
(3)假设存在垂直x轴的直线x=n,弦长为d
则
|
当m=1时不存在
当m>0且m≠1时,存在直线x=m-1
点评:本题以向量得数量积得坐标表示为载体考查了圆锥曲线得求解及直线与圆、圆锥曲线的位置关系得求解.属于综合试题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知点H(-3,0),点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且满足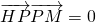 ,
,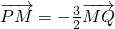 .
.
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点(1,0)作直线L交轨迹C于A、B两点,已知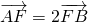 ,求直线L的方程.
,求直线L的方程.
已知点H(-3,0),点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且满足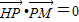 ,
,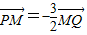 .
.
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点(1,0)作直线L交轨迹C于A、B两点,已知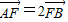 ,求直线L的方程.
,求直线L的方程.
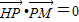 ,
,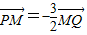 .
.(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点(1,0)作直线L交轨迹C于A、B两点,已知
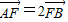 ,求直线L的方程.
,求直线L的方程.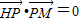 ,
,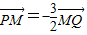 .
.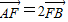 ,求直线L的方程.
,求直线L的方程.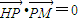 ,
,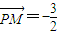
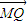 .
.
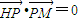 ,
,
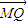 .
.