题目内容
 设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.
设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.(1)若A在距离中心5km的地方改变方向,建立适当坐标系,求:A改变方向后前进路径所在直线的方程
(2)设A、B两人速度一定,其速度比为3:1,且后来A恰与B相遇.问两人在何处相遇?(以村落中心为参照,说明方位和距离)
分析:(1)建立坐标系,设出直线方程,利用圆心到直线的距离等于5,即可求得直线方程;
(2)先确定PQ的斜率,设出直线方程,利用PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置,即可求得结论.
(2)先确定PQ的斜率,设出直线方程,利用PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置,即可求得结论.
解答: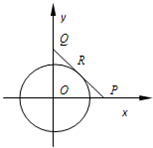 解:(1)建立如图坐标系,则P(5,0),
解:(1)建立如图坐标系,则P(5,0),
设直线方程为y=k(x-5)(k<0),由圆心到直线的距离等于5,可得
=3
∴k=±
,∵k<0,∴k=-
∴A改变方向后前进路径所在直线的方程为y=-
x+
;
(2)由题意可设A、B两人速度分别为3v千米/小时,v千米/小时,
再设A出发x0小时,在点P改变方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0,0),(0,vx0+vy0).
由|OP|2+|OQ|2=|PQ|2知,(3vx0)2+(vx0+vy0)2=(3vy0)2,
即(x0+y0)(5x0-4y0)=0.
∵x0+y0>0,∴5x0=4y0…①
将①代入kPQ=-
,∴kPQ=-
.
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线y=-
x+b与圆O:x2+y2=9相切,则有
=3,∴b=
.
答:A、B相遇点在村落中心正北距离
千米处
 解:(1)建立如图坐标系,则P(5,0),
解:(1)建立如图坐标系,则P(5,0),设直线方程为y=k(x-5)(k<0),由圆心到直线的距离等于5,可得
| |-5k| | ||
|
∴k=±
| 3 |
| 4 |
| 3 |
| 4 |
∴A改变方向后前进路径所在直线的方程为y=-
| 3 |
| 4 |
| 15 |
| 4 |
(2)由题意可设A、B两人速度分别为3v千米/小时,v千米/小时,
再设A出发x0小时,在点P改变方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0,0),(0,vx0+vy0).
由|OP|2+|OQ|2=|PQ|2知,(3vx0)2+(vx0+vy0)2=(3vy0)2,
即(x0+y0)(5x0-4y0)=0.
∵x0+y0>0,∴5x0=4y0…①
将①代入kPQ=-
| x0+y0 |
| 3x0 |
| 3 |
| 4 |
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线y=-
| 3 |
| 4 |
| |4b| | ||
|
| 15 |
| 4 |
答:A、B相遇点在村落中心正北距离
| 15 |
| 4 |
点评:本题考查直线方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.
设有半径为3km的圆形村落,A、B两人同时从村落中心出发.B一直向北直行;A先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝B所在的方向前进.