题目内容
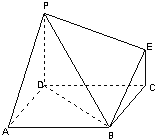 如图为一简单组合体,其底面 ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面 ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
(1)求证:BE∥平面PDA;
(2)求四棱锥B-CEPD的体积.
(1)证明:∵EC∥PD,PD?平面PDA,EC?平面PDA,∴EC∥平面PDA,
同理可得BC∥平面PDA----------(2分)
∵EC?平面EBC,BC?平面EBC且EC∩BC=C
∴平面BEC∥平面PDA-------(4分)
又∵BE?平面EBC,∴BE∥平面PDA-------(6分)
(2)解:∵PD⊥平面ABCD,PD?平面PDCE
∴平面PDCE⊥平面ABCD
∵BC⊥CD,平面PDCE∩平面ABCD=CD
∴BC⊥平面PDCE----------(8分)
∵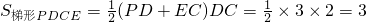 ------(10分)
------(10分)
∴四棱锥B-CEPD的体积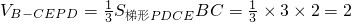 .----------(12分)
.----------(12分)
分析:(1)先证明线面平行,从而可得面面平行,进而可线面平行;
(2)先证明平面PDCE⊥平面ABCD,从而可得BC⊥平面PDCE,进而可求四棱锥B-CEPD的体积.
点评:本题考查面面平行、线面平行的判定与性质,考查四棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.
同理可得BC∥平面PDA----------(2分)
∵EC?平面EBC,BC?平面EBC且EC∩BC=C
∴平面BEC∥平面PDA-------(4分)
又∵BE?平面EBC,∴BE∥平面PDA-------(6分)
(2)解:∵PD⊥平面ABCD,PD?平面PDCE
∴平面PDCE⊥平面ABCD
∵BC⊥CD,平面PDCE∩平面ABCD=CD
∴BC⊥平面PDCE----------(8分)
∵
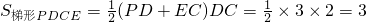 ------(10分)
------(10分)∴四棱锥B-CEPD的体积
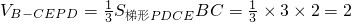 .----------(12分)
.----------(12分)分析:(1)先证明线面平行,从而可得面面平行,进而可线面平行;
(2)先证明平面PDCE⊥平面ABCD,从而可得BC⊥平面PDCE,进而可求四棱锥B-CEPD的体积.
点评:本题考查面面平行、线面平行的判定与性质,考查四棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.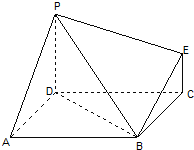 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,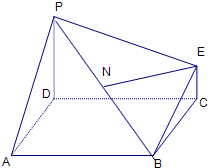 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC, 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.