题目内容
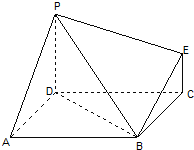 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:EN⊥平面PDB;
(3)若
| PD |
| AD |
| 2 |
分析:(1)由EC∥PD,根据线面平行的判定得:EC∥平面PDA,同时有BC∥平面PDA,再由面面平行的判定得平面BEC∥平面PDA,最后转化为线面平行.
(2)因为以D出发的三条线两两垂直,所以可以建立如图空间直角坐标系,利用向量法只要证明
•
=
×1-
×1-a×0=0,
•
=
×1-
×1+0×0=0即可.
(3)分别求得二个半平面的一个法向量即可,易知
为平面PBE的法向量,
为平面ABCD的法向量,分别求得其坐标,再用夹角公式求解即可.
(2)因为以D出发的三条线两两垂直,所以可以建立如图空间直角坐标系,利用向量法只要证明
| EN |
| PB |
| 1 |
| 2 |
| 1 |
| 2 |
| EN |
| DB |
| 1 |
| 2 |
| 1 |
| 2 |
(3)分别求得二个半平面的一个法向量即可,易知
| DN |
| DP |
解答: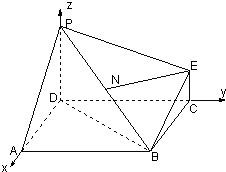 解:(1)证明:∵EC∥PD,PD?平面PDA,EC?平面PDA
解:(1)证明:∵EC∥PD,PD?平面PDA,EC?平面PDA
∴EC∥平面PDA,
同理可得BC∥平面PDA(2分)
∵EC?平面EBC,BC?平面EBC且EC∩BC=C
∴平面BEC∥平面PDA(3分)
又∵BE?平面EBC
∴BE∥平面PDA(4分)
(2)如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图示:
设该简单组合体的底面边长为1,PD=a
则B(1,1,0),C(0,1,0),P(0,0,a),E(0,1,
),N(
,
,
)(6分)
∴
=(
,-
,0),
=(1,1,-a),
=(1,1,0)
∵
•
=
×1-
×1-a×0=0,
•
=
×1-
×1+0×0=0
∴EN⊥PB,EN⊥DB(8分)
∵PB、DB?面PDB,且PB∩DB=B
∴NE⊥面PDB(9分)
(3)连接DN,由(2)知NE⊥面PDB∴DN⊥NE,
∵
=
,DB=
AD
∴PD=DB∴DN⊥PB
∴
为平面PBE的法向量,设AD=1,则N(
,
,
)
∴
=(
,
,
)(11分)
∵
为平面ABCD的法向量,
=(0,0,
),(12分)
设平面PBE与平面ABCD所成的二面角为θ,
则cosθ=
=
=
(13分)
∴θ=45°即平面PBE与平面ABCD所成的二面角为45°(4分)
 解:(1)证明:∵EC∥PD,PD?平面PDA,EC?平面PDA
解:(1)证明:∵EC∥PD,PD?平面PDA,EC?平面PDA∴EC∥平面PDA,
同理可得BC∥平面PDA(2分)
∵EC?平面EBC,BC?平面EBC且EC∩BC=C
∴平面BEC∥平面PDA(3分)
又∵BE?平面EBC
∴BE∥平面PDA(4分)
(2)如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图示:
设该简单组合体的底面边长为1,PD=a
则B(1,1,0),C(0,1,0),P(0,0,a),E(0,1,
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
∴
| EN |
| 1 |
| 2 |
| 1 |
| 2 |
| PB |
| DB |
∵
| EN |
| PB |
| 1 |
| 2 |
| 1 |
| 2 |
| EN |
| DB |
| 1 |
| 2 |
| 1 |
| 2 |
∴EN⊥PB,EN⊥DB(8分)
∵PB、DB?面PDB,且PB∩DB=B
∴NE⊥面PDB(9分)
(3)连接DN,由(2)知NE⊥面PDB∴DN⊥NE,
∵
| PD |
| AD |
| 2 |
| 2 |
∴PD=DB∴DN⊥PB
∴
| DN |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
| DN |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∵
| DP |
| DP |
| 2 |
设平面PBE与平面ABCD所成的二面角为θ,
则cosθ=
| ||||
|
|
| 1 | ||
|
| ||
| 2 |
∴θ=45°即平面PBE与平面ABCD所成的二面角为45°(4分)
点评:本题主要考查线线,线面,面面平行关系的转化,以及线面垂直,二面角的向量方法证明与求值,综合性较强,要求很熟练,属高档题.

练习册系列答案
相关题目
 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.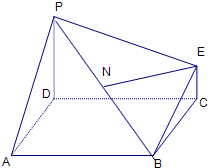 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC,
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC, 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.