题目内容
已知函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当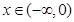 时,不等式
时,不等式 成立, 若
成立, 若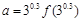 ,
,
 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
C
解析试题分析:构造函数h(x)=xf(x),
由函数y=f(x)以及函数y=x是R上的奇函数可得h(x)=xf(x)是R上的偶函数,
又当x∈(-∞,0)时h′(x)=f(x)+xf′(x)<0,
所以函数h(x)在x∈(-∞,0)时的单调性为单调递减函数;
所以h(x)在x∈(0,+∞)时的单调性为单调递增函数.
又因为函数y=f(x)是定义在R上的奇函数,所以f(0)=0,从而h(0)=0
因为log3 =-2,所以f(log3
=-2,所以f(log3 )=f(-2)=-f(2),
)=f(-2)=-f(2),
由0<logπ3<1<30.3<30.5<2,所以h(logπ3)<h(30.3)<h(2)=f(log3 ),即:
),即: ,故选C.
,故选C.
考点:对数函数的性质,函数的单调性,应用导数研究函数的单调性。
点评:中档题,比较大小问题,往往利用函数的单调性,而应用导数研究函数的单调性,是常见方法。本题关键是构造函数h(x)=xf(x)。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数 由
由 确定,则方程
确定,则方程 的实数解有( )
的实数解有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
三个数 的大小顺序是
的大小顺序是
| A.0.76<log0.76<60.7 | B.0.76<60.7<log0.76 |
| C.log0.76<60.7<0.76 | D. |
若 ,则
,则 的大小顺序是
的大小顺序是
A. | B. | C. | D.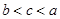 |
定义域为R的函数 满足
满足 时,
时, 若
若 时,
时, 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是
A. | B. |
C. | D. |
下列函数既是奇函数,又在区间 上单调递减的是( )
上单调递减的是( )
A.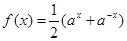 | B.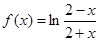 |
C.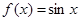 | D. |
设 ,则这四个数的大小关系是( )
,则这四个数的大小关系是( )
A. | B. |
C. | D.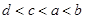 |
已知函数 在R上可导,且
在R上可导,且 ,则
,则 与
与 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D.不确定 |
已知函数 ,则
,则 ( )
( )
A. | B.9 | C. | D. |