题目内容
某企业实行裁员增效,已知现有员工201人,每人每年可创纯收益(已扣工资等)1万元,据评估在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的 ,设该企业裁员x人后年纯收益为y万元.
,设该企业裁员x人后年纯收益为y万元.(Ⅰ)写出y关于x的函数关系式,并指出x的取值范围;
(Ⅱ)问该企业应裁员多少人,才能获得最大的经济效益.
(注:在保证能取得最大经济效益的情况下,能少裁员,应尽量少裁)
【答案】分析:(Ⅰ)根据每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元的生活费,可的函数关系式,利用企业正常运转所需人数不得少于现有员工的 ,可求x的取值范围;
,可求x的取值范围;
(Ⅱ)利用配方法求最大的经济效益,应注意变量的范围及它是整数.
解答:解:(Ⅰ)由题意可得 y=(201-x)(1+0.01x)-0.4x=-0.01x2-0.61x+201
∵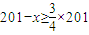 ,∴
,∴ ,即x的取值范围是
,即x的取值范围是 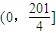
(Ⅱ)∵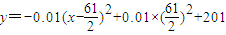
∴x=30时y取最大值
答:该企业应裁员30人,才能获得最大的经济效益.
点评:本题的考点是函数模型的选择与应用,主要考查二次函数模型,关键是将实际问题转化为数学问题,利用配方法求解二次函数的最值问题.
 ,可求x的取值范围;
,可求x的取值范围;(Ⅱ)利用配方法求最大的经济效益,应注意变量的范围及它是整数.
解答:解:(Ⅰ)由题意可得 y=(201-x)(1+0.01x)-0.4x=-0.01x2-0.61x+201
∵
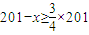 ,∴
,∴ ,即x的取值范围是
,即x的取值范围是 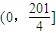
(Ⅱ)∵
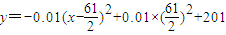
∴x=30时y取最大值
答:该企业应裁员30人,才能获得最大的经济效益.
点评:本题的考点是函数模型的选择与应用,主要考查二次函数模型,关键是将实际问题转化为数学问题,利用配方法求解二次函数的最值问题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,设该企业裁员x人后纯收益为y万元.
,设该企业裁员x人后纯收益为y万元. ,设该企业裁员x人后纯收益为y万元.
,设该企业裁员x人后纯收益为y万元. ,设该企业裁员x人后纯收益为y万元.
,设该企业裁员x人后纯收益为y万元.