题目内容
为应对国际金融危机对企业带来的不良影响，2009年某企业实行裁员增效，已知现有员工a人，每人每年可创纯利润1万元．据评估，在生产条件不变的条件下，每裁员1人，则留岗员工每人每年可多创收0.01万元，但每年需付给每位下岗工人0.4万元生活费，并且企业正常运行所需人数不得少于现有员工的
，设该企业裁员x人后纯收益为y万元．（1）写出y关于x的函数关系式，并指出x的取值范围；
（2）当140＜a≤280时，问企业裁员多少人，才能获得最大的经济效益？（注：在保证能获得最大经济效益的情况下，能少裁员，就尽量少裁）
【答案】分析：（1）根据该企业裁员x人后纯收益组成，即可得出：y=（a-x）（1+0.01x）-0.4x，∵
，即可得出x的取值范围是；
（2）依据（1）中所得的函数解析式，考虑当140＜a≤280时，分两类讨论：当a为偶数时，当a为奇数时，分析当x取何值时，y取最大值，从而确定企业裁员多少人．
解答：解：（1）y=（a-x）（1+0.01x）-0.4x=
∵
，
∴
，即x的取值范围是
，且x∈N．
（2）
，
当140＜a≤280时，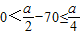
，
∴当a为偶数时，x取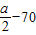
，y取最大值；
当a为奇数时，x取
或
，y取最大值．
∵尽可能少裁员，
∴x=
，
综上所述：当a为偶数时，应裁员
，
当a为奇数时，应裁员
．
点评：本小题主要考查函数模型的选择与应用以及运用函数的知识解决实际问题的能力，属于基础题．解决实际问题的关键是引进数学符号，建立数学模型．
，即可得出x的取值范围是；（2）依据（1）中所得的函数解析式，考虑当140＜a≤280时，分两类讨论：当a为偶数时，当a为奇数时，分析当x取何值时，y取最大值，从而确定企业裁员多少人．
解答：解：（1）y=（a-x）（1+0.01x）-0.4x=
∵
，∴
，即x的取值范围是，且x∈N．（2）
，当140＜a≤280时，
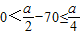，∴当a为偶数时，x取
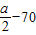，y取最大值；当a为奇数时，x取
或，y取最大值．∵尽可能少裁员，
∴x=
，综上所述：当a为偶数时，应裁员
，当a为奇数时，应裁员
．点评：本小题主要考查函数模型的选择与应用以及运用函数的知识解决实际问题的能力，属于基础题．解决实际问题的关键是引进数学符号，建立数学模型．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
，设该企业裁员x人后纯收益为y万元．
，设该企业裁员x人后纯收益为y万元．
，设该企业裁员x人后纯收益为y万元．