Question

直线l：x=my+n（n＞0）过点A（4，4

3

），若可行域

3 x-y≥0 x≤my+n y≥0

的外接圆直径为

16 3

3

，则实数n的值是

8

．

Answer 1

分析：令直线l：x=my+n（n＞0）与x轴交于B点，则得可行域是三角形OAB，根据正弦定理可构造一个关于n的方程，解方程即可求出实数n的值

解答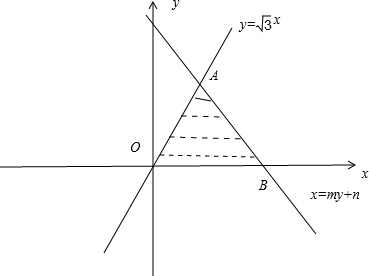：解：设直线l：x=my+n（n＞0）与x轴交于B（n，0）点，
∵直线x=my+n（n＞0）经过点A（4，4

3

），直线

3

x-y=0也经过点A（4，4

3

），
∴直线x=my+n（n＞0）经过一、二、四象限
∴m＜0
∴可行域是三角形OAB，且∠AOB=60°
∵可行域围成的三角形的外接圆的直径为

16 3

3

，
由正弦定理可得，

AB

sin60°

=2R=

16 3

3

∴AB=

16 3

3

•sin∠60°=8=

(n-4)2+(4 3 )2

∴n=8或0（舍去）
故答案为：8．

点评：本题考查的知识点是直线和圆的方程的应用，其中根据已知条件，结合正弦定理，构造关于n的方程，是解答本题关键．