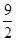题目内容
(本题12分)某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?


解:设需要甲种原料x张,乙种原料y张,
则可做文字标牌(x+2y)个,绘画标牌(2x+y)个.
由题意可得:
 …………5分
…………5分

所用原料的总面积为z=3x+2y,作出可行域如图,…………8分
在一组平行直线3x+2y=t中,经过可行域内的点且到原点距离最近的直线
过直线2x+y=5和直线x+2y=4的交点(2,1),∴最优解为:x=2,y=1………10分
∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.………12分
则可做文字标牌(x+2y)个,绘画标牌(2x+y)个.
由题意可得:
 …………5分
…………5分
所用原料的总面积为z=3x+2y,作出可行域如图,…………8分
在一组平行直线3x+2y=t中,经过可行域内的点且到原点距离最近的直线
过直线2x+y=5和直线x+2y=4的交点(2,1),∴最优解为:x=2,y=1………10分
∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.………12分
分析:本题考查的知识点是简单的线性规划的应用,根据已知条件中解:需要甲种原料x张,乙种原料y张,则可做文字标牌(x+2y)个,绘画标牌(2x+y)个,由题意得出约束条件,及目标函数,然后利用线性规划,求出最优解.
解答:

解:设需要甲种原料x张,乙种原料y张,
则可做文字标牌(x+2y)个,绘画标牌(2x+y)个.
由题意可得:
 …(5分)
…(5分)所用原料的总面积为z=3x+2y,作出可行域如图,…(8分)
在一组平行直线3x+2y=t中,经过可行域内的点且到原点距离最近的直线
过直线2x+y=5和直线x+2y=4的交点(2,1),∴最优解为:x=2,y=1…(10分)
∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.…(12分)
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 分)(理科)在线段AD上任取不同于A,D的两点B,C,在B,C处折断此线段得到一条折线。求此折线能构成三角形的概率。
分)(理科)在线段AD上任取不同于A,D的两点B,C,在B,C处折断此线段得到一条折线。求此折线能构成三角形的概率。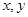 满足以下约束条件
满足以下约束条件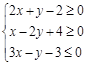 ,则
,则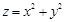 的最大值是 ( )
的最大值是 ( )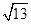
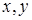 满足约束条件
满足约束条件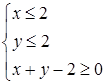 则
则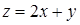 的最大值是 ;
的最大值是 ; 满足
满足 则
则 的最大值为______
的最大值为______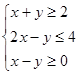 ,所围成的平面区域的面积为
,所围成的平面区域的面积为
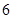
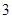
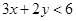 表示的平面区域内的点是 ( )
表示的平面区域内的点是 ( )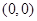
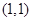
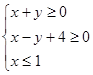 表示的平面区域面积是 ( )
表示的平面区域面积是 ( )