题目内容
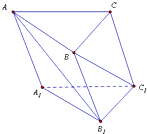 三菱柱ABC-A1B1C1中,底面边长和侧棱长都相等,∠BAA1=∠CAA1=600,则异面直线AB1与BC1所成角的余弦值为( )
三菱柱ABC-A1B1C1中,底面边长和侧棱长都相等,∠BAA1=∠CAA1=600,则异面直线AB1与BC1所成角的余弦值为( )分析:先选一组基底,再利用向量加法和减法的三角形法则和平行四边形法则将两条异面直线的方向向量用基底表示,
然后利用夹角公式求异面直线AB1与BC1所成角的余弦值即可.
然后利用夹角公式求异面直线AB1与BC1所成角的余弦值即可.
解答:解:如图, 设
设
=
,
=
,
=
,棱长均为1,
则
•
=
,
•
=
,
•
=
,
∵
=
+
,
=
-
+
,
∴
•
=(
+
)•(
-
+
)=
-1+
+
-
+1=1,
|
|=
=
=
=
,
|
|=
=
=
,
∴cos<
,
>=
=
∴异面直线AB1与BC1所成角的余弦值为
.
故选B.
 设
设| AA1 |
| c |
| AB |
| a |
| AC |
| b |
则
| a |
| b |
| 1 |
| 2 |
| b |
| c |
| 1 |
| 2 |
| a |
| c |
| 1 |
| 2 |
∵
| AB1 |
| a |
| c |
| BC1 |
| b |
| a |
| c |
∴
| AB1 |
| BC1 |
| a |
| c |
| b |
| a |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| AB1 |
(
|
|
| 1+1+1 |
| 3 |
|
| BC1 |
(
|
| 1+1+1-1+1-1 |
| 2 |
∴cos<
| AB1 |
| BC1 |
| 1 | ||||
|
| ||
| 6 |
∴异面直线AB1与BC1所成角的余弦值为
| ||
| 6 |
故选B.
点评:本题主要考查了空间向量在解决立体几何问题中的应用,考查空间向量基本定理,向量的数量积公式及应用,考查学生的计算能力.

练习册系列答案
相关题目
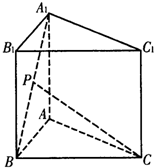 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB 如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2.
如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2. (2013•四川)如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
(2013•四川)如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.