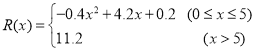题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 时,
时,![]() .
.

(1)求函数![]() 的解析式,并画出函数图像;
的解析式,并画出函数图像;
(2)写出函数![]() 的单调区间及值域;
的单调区间及值域;
(3)求使![]() 恒成立的实数
恒成立的实数![]() 的取值范围.
的取值范围.
(注明:(2)(3)可直接写出答案,不要求写出解答过程)
【答案】(1)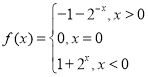 ;(2)
;(2)![]() 的单调递增区间为
的单调递增区间为![]() ,值域为
,值域为![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据奇函数的性质,结合函数在![]() 时的解析式,可得
时的解析式,可得![]() 在
在![]() 上的解析式;根据指数函数的图象以及平移的相关知识可先作出
上的解析式;根据指数函数的图象以及平移的相关知识可先作出![]() 时的图象,再根据奇函数的性质作出
时的图象,再根据奇函数的性质作出![]() 时的图象;(2)根据函数的图象可得函数的单调区间,值域;(3)根据函数的图象可得函数的最小值.
时的图象;(2)根据函数的图象可得函数的单调区间,值域;(3)根据函数的图象可得函数的最小值.
试题解析:(1)设![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
∴![]() ,且
,且![]() ,
,
![]() ,即
,即![]() ,
,
![]() 函数
函数![]() 的解析式为
的解析式为 ........4分
........4分
(2)由图可知,函数![]() 的单调递增区间为
的单调递增区间为![]() ;........... 8分
;........... 8分
值域为![]() ................10分
................10分
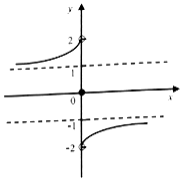
(3)由图可知,要使![]() 恒成立,实数
恒成立,实数![]() 的取值范围为
的取值范围为![]() .........12分
.........12分

练习册系列答案
相关题目
【题目】某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此判断哪组工人的技术水平更好;
(2)质监部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,否则“不合格”.求该车间“质量不合格”的概率.