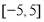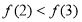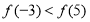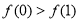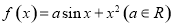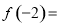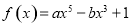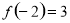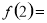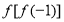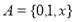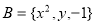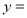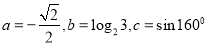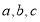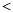题目内容
已知二次函数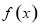 满足
满足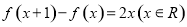 ,且
,且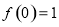 。
。
(1)求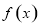 的解析式;
的解析式;
(2)当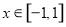 时,方程
时,方程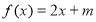 有解,求实数
有解,求实数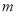 的取值范围;
的取值范围;
(3)设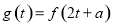 ,
,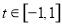 ,求
,求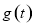 的最大值.
的最大值.
【解析】
试题分析:(1)设出二次函数的一般形式后,代入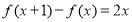 ,化简后根据多项式相等,各系数相等即可求出
,化简后根据多项式相等,各系数相等即可求出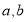 及
及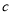 的值,即可确定出
的值,即可确定出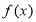 的解析式;
的解析式;
(2)不等式有解即为把不等式变为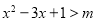 有解,令
有解,令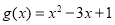 ,求出
,求出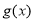 在区间
在区间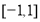 上的值域,即可得到
上的值域,即可得到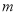 的取值范围,
的取值范围,
(3)把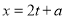 代入
代入 的解析式中即可表示出
的解析式中即可表示出 的函数关系式,由二次函数求对称轴的方法表示出
的函数关系式,由二次函数求对称轴的方法表示出 的对称轴,根据对称轴大于等于
的对称轴,根据对称轴大于等于 和小于
和小于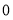 ,分两种情况考虑,分别画出相应的函数图象,根据函数的图象即可分别得到
,分两种情况考虑,分别画出相应的函数图象,根据函数的图象即可分别得到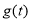 的最大值,并求出相应
的最大值,并求出相应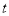 的范围,联立即可得到
的范围,联立即可得到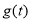 最大值与
最大值与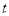 的分段函数解析式.
的分段函数解析式.
试题解析:【解析】
(1)设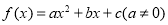
代入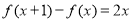 和
和
并化简得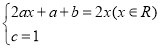 ,
,
(2)当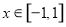 时,方程
时,方程 有解
有解
即方程 在上
在上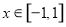 有解
有解
令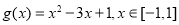 ,则
,则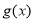 的值域是
的值域是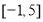
故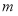 的取值范围是
的取值范围是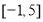
(3)
对称轴是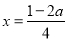 。
。
①当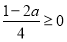 时,即
时,即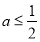 时
时
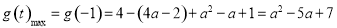 ;
;
② 当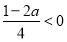 时,即
时,即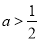 时,
时,
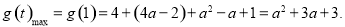
综上所述:。

考点:考查函数的解析式,二次函数的图象与性质及不等式恒成立时所满足的条件,考查了分类讨论的数学思想,是一道综合题.

练习册系列答案
相关题目