题目内容
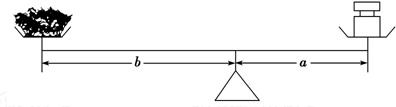
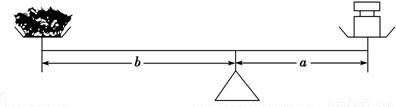
某药店有一架不准确的天平(其左右两臂不等长)和一个50克的砝码.一名顾客想要购买100克中药,营业员便分两次为他称量.第一次,他将砝码放在左盘中,将药物放在右盘中,待平衡后将药物交给顾客;第二次,他将药物放在左盘中,将砝码放在右盘中,待平衡后将药物交给顾客.问,营业员这样称量,顾客实际得到的药物是否正好是100克?说明理由(不考虑其他因素造成的误差).
【答案】分析:设天平左臂长为a,右臂长为b,由已知,a≠b,又设营业员第一次和第二次称量的药物重量分别为x克和y克.根据两次天平平衡,列出两个等量关系,利用基本不等式即可解决.
解答:解:设天平左臂长为a,右臂长为b,由已知,a≠b,又设营业员第一次和第二次称量的药物重量分别为x克和y克.
则有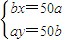 ,…(6分) 所以
,…(6分) 所以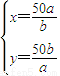 ,…(8分)
,…(8分)
于是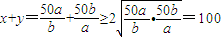 ,当且仅当a=b时等号成立.…(10分)
,当且仅当a=b时等号成立.…(10分)
因为a≠b,所以x+y>100,即顾客实际得到的药物超过100克.…(12分)
点评:本题考查不等关系与不等式的应用,解题的关键是灵活运用基本不等式,属于基础题.
解答:解:设天平左臂长为a,右臂长为b,由已知,a≠b,又设营业员第一次和第二次称量的药物重量分别为x克和y克.
则有
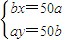 ,…(6分) 所以
,…(6分) 所以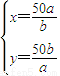 ,…(8分)
,…(8分)于是
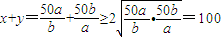 ,当且仅当a=b时等号成立.…(10分)
,当且仅当a=b时等号成立.…(10分)因为a≠b,所以x+y>100,即顾客实际得到的药物超过100克.…(12分)
点评:本题考查不等关系与不等式的应用,解题的关键是灵活运用基本不等式,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 某药店有一架不准确的天平(其左右两臂不等长)和一个50克的砝码.一名顾客想要购买100克中药,营业员便分两次为他称量.第一次,他将砝码放在左盘中,将药物放在右盘中,待平衡后将药物交给顾客;第二次,他将药物放在左盘中,将砝码放在右盘中,待平衡后将药物交给顾客.问,营业员这样称量,顾客实际得到的药物是否正好是100克?说明理由(不考虑其他因素造成的误差).
某药店有一架不准确的天平(其左右两臂不等长)和一个50克的砝码.一名顾客想要购买100克中药,营业员便分两次为他称量.第一次,他将砝码放在左盘中,将药物放在右盘中,待平衡后将药物交给顾客;第二次,他将药物放在左盘中,将砝码放在右盘中,待平衡后将药物交给顾客.问,营业员这样称量,顾客实际得到的药物是否正好是100克?说明理由(不考虑其他因素造成的误差).