题目内容
设函数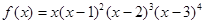 ,则函数
,则函数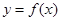 的极大值点为( )
的极大值点为( )
A.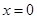 | B.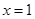 | C.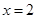 | D.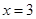 |
B
解析试题分析:当0<x<1时,f(x)=x(x-1)2(x-2)3(x-3)4<0,
当x=1时,f(x)=x(x-1)2(x-2)3(x-3)4=0,
当1<x<2时,f(x)=x(x-1)2(x-2)3(x-3)4<0,
其函数f(x)=x(x-1)2(x-2)3(x-3)4大致如图所示.
结合图象可知,当0<x<1时,函数是增,当1<x<2时,函数是减函数,
根据函数极值的概念可知,x=1是函数y=f(x)的极大值点.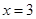 是极小值点,
是极小值点,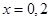 不是极值点。故选B.
不是极值点。故选B.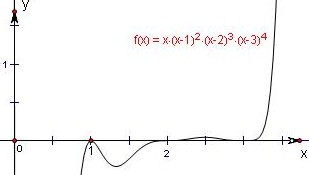
考点:极值点的概念及判断
点评:中档题,画出函数的图象,不是件容易的事,因此,通过分析函数图象的大致形态,可以判断极值点。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
函数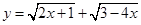 的定义域为( )
的定义域为( )
A.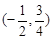 | B.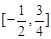 |
C.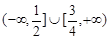 | D.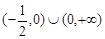 |
定义在区间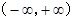 上的奇函数
上的奇函数 为增函数,偶函数
为增函数,偶函数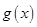 在
在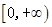 上图象与
上图象与 的图象重合.设
的图象重合.设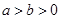 ,给出下列不等式,其中成立的是( )
,给出下列不等式,其中成立的是( )
①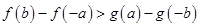
②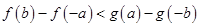
③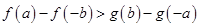
④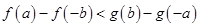
| A.①④ | B.②③ | C.①③ | D.②④ |
已知函数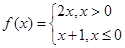 ,若f(a)+f(1)=0,则实数a的值等于( )
,若f(a)+f(1)=0,则实数a的值等于( )
| A.3 | B.1 | C.-1 | D.-3 |
设函数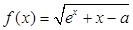 (
(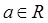 ,
,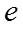 为自然对数的底数).若存在
为自然对数的底数).若存在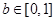 使
使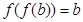 成立,则
成立,则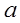 的取值范围是
的取值范围是
A.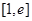 | B.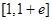 | C.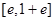 | D.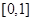 |
设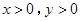 ,定义
,定义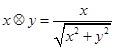 ,则
,则 +2
+2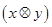
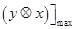 等于( )
等于( )
A.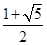 | B.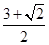 |
C.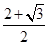 | D.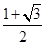 |
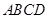 中,
中,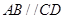 ,且
,且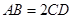 ,设
,设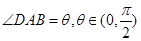 ,以
,以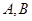 为焦点且过点
为焦点且过点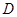 的双曲线的离心率为
的双曲线的离心率为 ,以
,以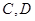 为焦点且过点
为焦点且过点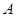 的椭圆的离心率为
的椭圆的离心率为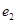 ,设
,设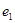 =
=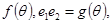 则
则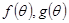 的大致图像是( )
的大致图像是( )
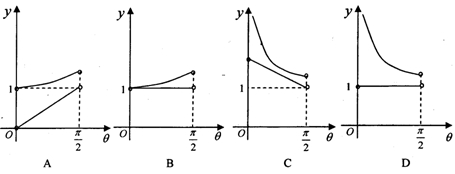
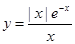 的图像的大致形状是( )
的图像的大致形状是( )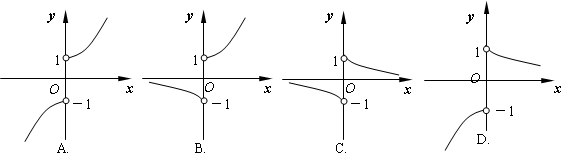
 ,当
,当 时,
时, 取得最小值
取得最小值 ,则函数
,则函数 的图象为( )
的图象为( )