题目内容
已知函数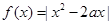
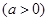 ,
,
(1)当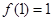 时,
求
时,
求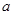 的值;
的值;
(2)若函数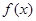 在
在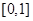 上的最大值为
上的最大值为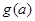
(ⅰ)求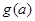 的解析式;
的解析式;
(ⅱ)对任意的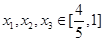 ,以
,以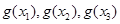 的值为边长的三条线段是否可构成三角形?请说明理由。
的值为边长的三条线段是否可构成三角形?请说明理由。
【答案】
解:1)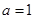 ;(2)
;(2) 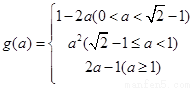 ;
;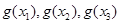 的值为边长的三条线段可构成三角形.
的值为边长的三条线段可构成三角形.
【解析】分类讨论函数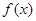 在
在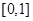 上单调性,数形结合;三条线段是否可构成三角形关键判断两边之和是否大于第三边。
上单调性,数形结合;三条线段是否可构成三角形关键判断两边之和是否大于第三边。
解:1)、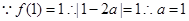 或
或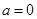 (舍去)
(舍去)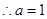
(2)(ⅰ)当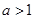 时,如图(1),
时,如图(1),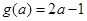
当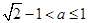 时,如图(2),
时,如图(2),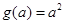
当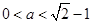 时,如图(2),
时,如图(2),
 |
|||||||||||
 |
 |
||||||||||
 |
 |
 |
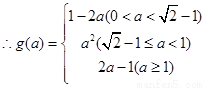
ⅱ)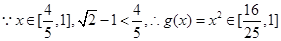 ,
,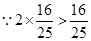
所以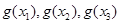 的值为边长的三条线段可构成三角形
的值为边长的三条线段可构成三角形

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,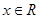 .
.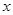 为何值时,
为何值时,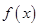 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
,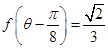 ,求
,求 的值.
的值.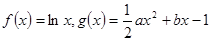 ,
, 且
且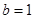 时,证明:对
时,证明:对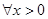 ,
,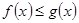 ;
;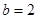 ,且
,且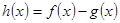 存在单调递减区间,求
存在单调递减区间,求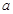 的取值范围;
的取值范围;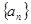 ,若存在常数
,若存在常数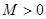 ,
,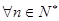 ,都有
,都有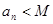 ,则称数列
,则称数列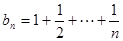 ,试判断数列
,试判断数列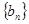 是否有上界.
是否有上界.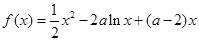 ,
,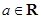 .
.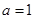 时,求函数
时,求函数 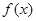 的最小值;
的最小值; 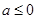 时,讨论函数
时,讨论函数 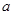 ,对任意的
,对任意的
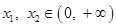 ,且
,且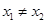 ,有
,有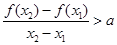 ,恒成立,若存在求出
,恒成立,若存在求出