题目内容
(本小题满分14分)
在直角坐标系xOy中,已知圆心在第二象限、半径为2 的圆C与直线y=x相切于
的圆C与直线y=x相切于
坐标原点O.椭圆 与圆C的一个交点到椭圆两焦点的距离之和为10。
与圆C的一个交点到椭圆两焦点的距离之和为10。
(1)求圆C的方程;

 (2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段
OF的长,若存在求出Q的坐标;若不存在,请说明理由。
在直角坐标系xOy中,已知圆心在第二象限、半径为2
 的圆C与直线y=x相切于
的圆C与直线y=x相切于坐标原点O.椭圆
 与圆C的一个交点到椭圆两焦点的距离之和为10。
与圆C的一个交点到椭圆两焦点的距离之和为10。(1)求圆C的方程;

 (2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段
(2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆的右焦点F的距离等于线段OF的长,若存在求出Q的坐标;若不存在,请说明理由。
+ =1
(1)设圆心坐标为(m,n)(m<0,n>0),则该圆的方程为(x-m)2+(y-n)2=8
已知该圆与直线y=x相切,那么圆心到该直线的距离等于圆的半径,则
 =2
=2
即 ="4 " ①
="4 " ①
又圆与直线切于原点,将点(0,0)代入得
m2+n2="8 " ②
联立方程①和②组成方程组解得


 故圆的方程为(x+2)2+(y-2)2=8
故圆的方程为(x+2)2+(y-2)2=8
(2) =5,∴a2=25,则椭圆的方程为 + =1
=5,∴a2=25,则椭圆的方程为 + =1
其焦距c= =4,右焦点为(4,0),那么
=4,右焦点为(4,0),那么 =4。
=4。
要探求是否存在异于原点的点Q,使得该点到右焦点F的距离等于 的长度4,我们可以转化为探求以右焦点F为顶点,半径为4的圆(x─4)2+y2=8与(1)所求的圆的交点数。通过联立两圆的方程解得x=
的长度4,我们可以转化为探求以右焦点F为顶点,半径为4的圆(x─4)2+y2=8与(1)所求的圆的交点数。通过联立两圆的方程解得x= ,y=
,y= 即存在异于原点的点Q(
即存在异于原点的点Q( ,
, ),使得该点到右焦点F的距离等于
),使得该点到右焦点F的距离等于 的长。
的长。
已知该圆与直线y=x相切,那么圆心到该直线的距离等于圆的半径,则
 =2
=2
即
 ="4 " ①
="4 " ① 又圆与直线切于原点,将点(0,0)代入得
m2+n2="8 " ②
联立方程①和②组成方程组解得


 故圆的方程为(x+2)2+(y-2)2=8
故圆的方程为(x+2)2+(y-2)2=8(2)
 =5,∴a2=25,则椭圆的方程为 + =1
=5,∴a2=25,则椭圆的方程为 + =1其焦距c=
 =4,右焦点为(4,0),那么
=4,右焦点为(4,0),那么 =4。
=4。要探求是否存在异于原点的点Q,使得该点到右焦点F的距离等于
 的长度4,我们可以转化为探求以右焦点F为顶点,半径为4的圆(x─4)2+y2=8与(1)所求的圆的交点数。通过联立两圆的方程解得x=
的长度4,我们可以转化为探求以右焦点F为顶点,半径为4的圆(x─4)2+y2=8与(1)所求的圆的交点数。通过联立两圆的方程解得x= ,y=
,y= 即存在异于原点的点Q(
即存在异于原点的点Q( ,
, ),使得该点到右焦点F的距离等于
),使得该点到右焦点F的距离等于 的长。
的长。
练习册系列答案
相关题目
 与
与 ,其观测值的
,其观测值的 列联表如下:
列联表如下:

 合计
合计





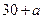
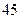



 的整数,若
的整数,若 时,有
时,有 的把握认为两个分类变量
的把握认为两个分类变量
 .根据表中数据,得到
.根据表中数据,得到 , 则认为选修文科与性别有关系出错的可能性是( )
, 则认为选修文科与性别有关系出错的可能性是( ) ,则a等于 ( )
,则a等于 ( )



 学
学