题目内容
设函数 .(I)求函数
.(I)求函数 的单调递增区间;
的单调递增区间;
(II) 若关于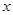 的方程
的方程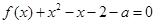 在区间
在区间 内恰有两个不同的实根,求实数
内恰有两个不同的实根,求实数 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 的取值范围是
的取值范围是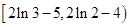
解析试题分析:(Ⅰ)求出导数,根据导数大于0求得 的单调递增区间.
的单调递增区间.
(Ⅱ)令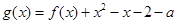 .利用导数求出
.利用导数求出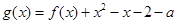 的单调区间和极值点,画出其简图,结合函数零点的判定定理找出
的单调区间和极值点,画出其简图,结合函数零点的判定定理找出 所满足的条件,由此便可求出
所满足的条件,由此便可求出 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数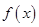 的定义域为
的定义域为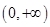 ,
,
∵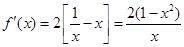 ,
,
∵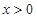 ,则使
,则使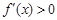 的
的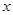 的取值范围为
的取值范围为 ,
,
故函数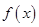 的单调递增区间为
的单调递增区间为
(Ⅱ)∵ ,
,
∴
令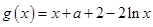 ,
,
∵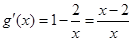 ,且
,且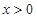 ,
,
由 得
得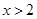 ,由
,由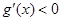 得
得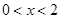 .
.
∴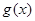 在区间
在区间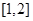 内单调递减,在区间
内单调递减,在区间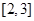 内单调递增,
内单调递增,
故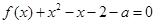 在区间
在区间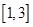 内恰有两个相异实根
内恰有两个相异实根 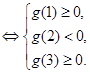
即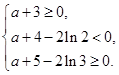 解得:
解得: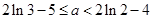 .
.
综上所述, 的取值范围是
的取值范围是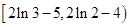
考点:1、导数及其应用;2、函数的零点.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 (
( 为常数)的图象过原点,且对任意
为常数)的图象过原点,且对任意 总有
总有 成立;
成立; 的最大值等于1,求
的最大值等于1,求 与
与 的大小关系.
的大小关系. 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
. ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 ; ②
; ②
 且
且 .
. 的值;
的值; 在
在 上的单调性,并给予证明.
上的单调性,并给予证明. ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根. 的解析式;
的解析式;
 时,求函数
时,求函数 的表达式.
的表达式. (其中
(其中 )的图象如图所示.
)的图象如图所示.
 的解析式;
的解析式; ,且
,且 ,求
,求 的单调区间.
的单调区间. 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.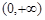 上的单调性.
上的单调性. ,
,
 .
. ,求函数
,求函数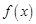 在区间
在区间 上的最值;
上的最值; 恒成立,求
恒成立,求 的取值范围. (注:
的取值范围. (注: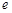 是自然对数的底数)
是自然对数的底数) 的函数
的函数 ,其导函数为
,其导函数为 .若对
.若对 ,均有
,均有 ,则称函数
,则称函数 ,试判断
,试判断 是否为其定义域上的梦想函数,并说明理由;
是否为其定义域上的梦想函数,并说明理由; (
( ,
, )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求 的取值范围;
的取值范围; (
( )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求