题目内容
已知数列 的前
的前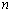 项和为
项和为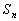 ,
, ,且
,且 (
(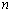 为正整数)
为正整数)
(Ⅰ)求出数列 的通项公式;
的通项公式;
(Ⅱ)若对任意正整数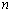 ,
, 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
【答案】
解:(Ⅰ)
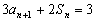 , ①
, ①  当
当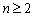 时,
时,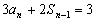 . ② ……(1分)
. ② ……(1分)
由 ① - ②,得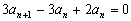 .
……………………(2分)
.
……………………(2分)
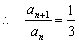
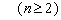 .
……………………(3分)
.
……………………(3分)
又 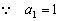 ,
,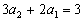 ,解得
,解得 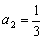 . …… (4分)
. …… (4分)
 数列
数列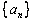 是首项为1,公比为
是首项为1,公比为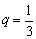 的等比数列.
的等比数列.
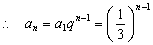 (
(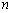 为正整数)……………………(6分)
为正整数)……………………(6分)
(Ⅱ)由(Ⅰ)知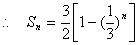 …………………(8分)
…………………(8分)
由题意可知,对于任意的正整数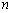 ,恒有
,恒有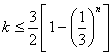 ,.
,.
 数列
数列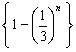 单调递增, 当
单调递增, 当 时,数列中的最小项为
时,数列中的最小项为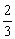 , …(10分)
, …(10分)
 必有
必有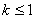 ,即实数
,即实数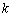 的最大值为1 ……………… (12分)
的最大值为1 ……………… (12分)

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式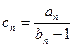 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.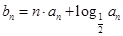 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.