Question

定义：对于各项均为整数的数列，如果(=1，2，3， )为完全平方数，则称数列具有“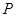性质”；不论数列是否具有“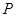性质”，如果存在数列与不是同一数列，且满足下面两个条件：

（1）是的一个排列；

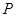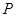（2）数列具有“性质”，则称数列具有“变换性质”．

给出下面三个数列：

①数列的前项和；

②数列：1，2，3，4，5；

③数列：1，2，3，4，5，6，7，8，9，10，11.

具有“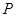性质”的为        ；具有“变换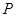性质”的为           .

 

Answer 1

【答案】

①、②

【解析】

试题分析：对于①，求出数列{a_n}的通项，验证a_i+i=i²（i=1，2，3，…）为完全平方数，可得结论；对于②，数列1，2，3，4，5，具有“变换P性质”，数列{b_n}为3，2，1，5，4，具有“P性质”；对于③，因为11，4都只有与5的和才能构成完全平方数，所以1，2，3，…，11，不具有“变换P性质”． 解：对于①，当n≥2时，a_n=S_n-S_n-1=n²-n，∵a₁=0，∴a_n=n²-n，∴a_i+i=i²（i=1，2，3，…）为完全平方数，∴数列{a_n}具有“P性质”；，对于②，数列1，2，3，4，5，具有“变换P性质”，数列{b_n}为3，2，1，5，4，具有“P性质”，∴数列{a_n}具有“变换P性质”；，对于③，因为11，4都只有与5的和才能构成完全平方数，所以1，2，3，…，11，不具有“变换P性质”．，故答案为：①，②．

考点：新定义

点评：本题考查新定义，考查学生分析解决问题的能力，正确理解新定义是关键．