题目内容
对于各项均为正数且各有m项的数列{an},{bn},按如下方法定义数列{tn}:t=0, (n=1,2…m),并规定数列{an}到{bn}的“并和”为Sab=a1+a2+…+an+tm.
(n=1,2…m),并规定数列{an}到{bn}的“并和”为Sab=a1+a2+…+an+tm.(Ⅰ)若m=3,数列{an}为3,7,2;数列{bn}为5,4,6,试求出t1、t2、t3的值以及数列{an}到{bn}的并和Sab;
(Ⅱ)若m=4,数列{an}为3,2,3,4;数列{bn}为6,1,x,y,且Sab=17,求证:y≤5;
(Ⅲ)若m=6,下表给出了数列{an},{bn}:

如果表格中各列(整列)的顺序可以任意排列,每种排列都有相应的并和Sab,试求Sab的最小值,并说明理由.
【答案】分析:(Ⅰ)由数列{tn}的定义可知:令n=1,2,3可求得t1、t2、t3的值以及数列{an}到{bn}的并和Sab;
(Ⅱ)数列{an}为3,2,3,4;且Sab=17,求出t4,根据数列{tn}的定义,可求得t1、t2、t3的值,比较t3和t4的大小,即可证明y≤5;
(Ⅲ)当1≤n≤6时,由(Ⅱ)知tn=max{bn,tn-1-an+bn},则tn≥tn-1-an+bn,即tn-tn-1≥bn-an,采用累加法即可求得关于Sab的不等式,分类讨论求得其最小值.
解答:解:(Ⅰ)由数列{tn}的定义可知:t1=b1=5,
t2=b2=4,
t3=t2-a3+b3=8,
Sab=a1+a2+a3+t3=20.
(Ⅱ)证明:由Sab=17,得t4=Sab-(a1+a2+a3+a4)=5.
而t1=b1=6,t2=t1-a2+b2=5,t3=t2-a3+b3=x+2,
当t3<a4,即x<2t4=b4=y,则y=5
t3≥a4即x≥2有t4=t3-a4+b4=x-2+y,则y=7-x≤7-2=5,
综上所述,必有y≤5成立.
(Ⅲ)Sab的最小值为51,当表格如下排列(记作排列※)时可取到:
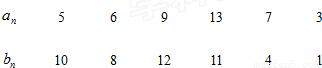
当1≤n≤6时,由(Ⅱ)知tn=max{bn,tn-1-an+bn},
则tn≥tn-1-an+bn,即tn-tn-1≥bn-an.于是
t6-t5≥b6-a6,
t5-t4≥b5-a5,
t4-t3≥b4-a4,
t3-t2≥b3-a3,
t2-t1≥b2-a2.
将上述不等式相加得:
t6-t1≥(b2+b3+…+b6)-(a2+a3+…+a6).
∵Sab=(a1+a2+a3+…+a6)+t6.
∴Sab≥(a1+a2+…+a6)+t1+(b2+b3+…+b6)-(a2+a3+…+a6).
∴Sab≥a1+b1+(b2+b3+…+b6)=46+a1.①
将前4个不等式相加得t6-t2≥(b3+b4+b5++b6)-(a3+a4+a5+a6).
类似地,可整理得Sab≥t2+(46-b1-b2)+a1+a2.②
若a1≠3,可见a1≥5,由①得Sab≥46+a1≥51;
若a1=3,则b1=1,那么t1=b1=1<a2,故t1=b2.
此时由②得Sab≥t2+(46-b1-b2)+a1+a2=46-b1+a1+a2=48+a2≥53.
综上所述,Sab≥51总是成立的.
点评:考查学生理解数列概念,灵活运用数列表示法的能力,旨在考查学生的观察分析和归纳能力,特别是问题(Ⅲ)的设置,增加了题目的难度,同时也考查了分类讨论的思想,属难题.
(Ⅱ)数列{an}为3,2,3,4;且Sab=17,求出t4,根据数列{tn}的定义,可求得t1、t2、t3的值,比较t3和t4的大小,即可证明y≤5;
(Ⅲ)当1≤n≤6时,由(Ⅱ)知tn=max{bn,tn-1-an+bn},则tn≥tn-1-an+bn,即tn-tn-1≥bn-an,采用累加法即可求得关于Sab的不等式,分类讨论求得其最小值.
解答:解:(Ⅰ)由数列{tn}的定义可知:t1=b1=5,
t2=b2=4,
t3=t2-a3+b3=8,
Sab=a1+a2+a3+t3=20.
(Ⅱ)证明:由Sab=17,得t4=Sab-(a1+a2+a3+a4)=5.
而t1=b1=6,t2=t1-a2+b2=5,t3=t2-a3+b3=x+2,
当t3<a4,即x<2t4=b4=y,则y=5
t3≥a4即x≥2有t4=t3-a4+b4=x-2+y,则y=7-x≤7-2=5,
综上所述,必有y≤5成立.
(Ⅲ)Sab的最小值为51,当表格如下排列(记作排列※)时可取到:
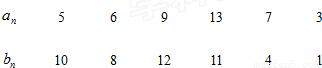
当1≤n≤6时,由(Ⅱ)知tn=max{bn,tn-1-an+bn},
则tn≥tn-1-an+bn,即tn-tn-1≥bn-an.于是
t6-t5≥b6-a6,
t5-t4≥b5-a5,
t4-t3≥b4-a4,
t3-t2≥b3-a3,
t2-t1≥b2-a2.
将上述不等式相加得:
t6-t1≥(b2+b3+…+b6)-(a2+a3+…+a6).
∵Sab=(a1+a2+a3+…+a6)+t6.
∴Sab≥(a1+a2+…+a6)+t1+(b2+b3+…+b6)-(a2+a3+…+a6).
∴Sab≥a1+b1+(b2+b3+…+b6)=46+a1.①
将前4个不等式相加得t6-t2≥(b3+b4+b5++b6)-(a3+a4+a5+a6).
类似地,可整理得Sab≥t2+(46-b1-b2)+a1+a2.②
若a1≠3,可见a1≥5,由①得Sab≥46+a1≥51;
若a1=3,则b1=1,那么t1=b1=1<a2,故t1=b2.
此时由②得Sab≥t2+(46-b1-b2)+a1+a2=46-b1+a1+a2=48+a2≥53.
综上所述,Sab≥51总是成立的.
点评:考查学生理解数列概念,灵活运用数列表示法的能力,旨在考查学生的观察分析和归纳能力,特别是问题(Ⅲ)的设置,增加了题目的难度,同时也考查了分类讨论的思想,属难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
