题目内容
4.△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,已知向量$\overrightarrow{m}$=(a,btanA),$\overrightarrow{n}$=(b,atanB),若$\overrightarrow{m}$∥$\overrightarrow{n}$,试判定△ABC的形状.分析 通过向量的共线结合正弦定理以及同角三角函数的基本关系式化简即可得到结果.
解答 解:向量$\overrightarrow{m}$=(a,btanA),$\overrightarrow{n}$=(b,atanB),$\overrightarrow{m}$∥$\overrightarrow{n}$,
知a2tanB=b2tanA,即a2sinBcosA=b2sinAcosB,
利用正弦定理化简得:sinAcosA=sinBcosB,即sin2A=sin2B,
又A,B∈(0,π),0<A+B<π,
∴2A=2B,或2A+2B=π,即A=B或A+B=$\frac{π}{2}$,
则△ABC为等腰三角形或直角三角形;
点评 此题属于解三角形的题型,涉及的知识有:平面向量的数量积运算,正弦定理,二倍角的正弦函数公式,以及正弦、余弦函数的图象与性质,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
14.下表是某地一年中10天测量得白昼时间统计表(时间近似0.1小时,一年按365天计).
(1)以日期在365一天中得位置序号x为横坐标,白昼时间y为纵坐标,在给定的坐标中,试选用一个形如y=Asin(ωx+φ)+t的函数来近似描述一年中,白昼时间y与日期位置序号x之间的函数关系;
(2)用(1)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
| 日期 | 1月1日 | 2月28日 | 3月21日 | 4月27日 | 5月6日 | 6月21日 | 8月13日 | 9月20日 | 10月25日 | 12月21日 |
| 日期位置序号x | 1 | 59 | 80 | 117 | 126 | 172 | 225 | 268 | 298 | 355 |
| 白昼时间y(小时) | 5.6 | 10.2 | 12.4 | 16.4 | 17.3 | 19.4 | 16.4 | 12.4 | 8.5 | 5.4 |
(2)用(1)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
9.三条不重合的直线a,b,c及三个不重合的平面α,β,γ,下列命题正确的是( )
| A. | 若a∥α,a∥β,则α∥β | B. | 若α∩β=a,α⊥γ,β⊥γ,则a⊥γ | ||
| C. | 若a?α,b?α,c?β,c⊥a,c⊥b,则α⊥β | D. | 若α∩β=a,c?γ,c∥α,c∥β,则a∥γ |
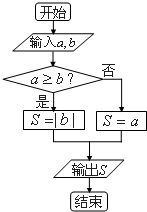 定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为2.
定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为2.