题目内容
4.已知函数f(x)=e2x,g(x)=$\frac{1}{1-x}$(x2-ax-2xsinx+1),x∈[-1,0].(Ⅰ)求证:$\frac{1+x}{1-x}$≤f(x)≤$\frac{1}{(1-x)^{2}}$;
(Ⅱ)若?x∈[-1,0],使得f(x)≥g(x)恒成立,求实数a取值范围.
分析 (Ⅰ)问题转化为证(1+x)e-x≤(1-x)ex,导数法可判h(x)=(1+x)e-x-(1-x)ex在x∈[-1,0]上单调递增,可证f(x)≥$\frac{1+x}{1-x}$,同理可证f(x)≤$\frac{1}{(1-x)^{2}}$,综合可得;
(Ⅱ)由(Ⅰ)可知1+x≤e2x(1-x)≤$\frac{1}{1-x}$,可得设m(x)=f(x)-g(x)≥$\frac{x}{1-x}$(1+a-x+2sinx),令l(x)=-x+2sinx,可判l(x)在x∈[-1,0]上是增函数,可得a≤-1时,f(x)≥g(x)恒成立,同理证明当a>-1时,f(x)≥g(x)不恒成立,综合可得实数a取值范围.
解答 (Ⅰ)证明:要证x∈[-1,0]时,e2x≥$\frac{1+x}{1-x}$,只需证(1+x)e-x≤(1-x)ex,
记h(x)=(1+x)e-x-(1-x)ex,则h′(x)=x(ex-e-x)≥0,x∈[-1,0],
∴h(x)在x∈[-1,0]上单调递增,∴h(x)≤h(0)=0,∴f(x)≥$\frac{1+x}{1-x}$,
要证x∈[-1,0]时,e2x≤$\frac{1}{(1-x)^{2}}$,只需证ex≤$\frac{1}{1-x}$,即证1-x≤e-x,
记k(x)=1-x-e-x,则k′(x)=-1+e-x≥0,
∴k(x)在x∈[-1,0]上单调递增,
∴k(x)≤k(0)=0,即f(x)≤$\frac{1}{(1-x)^{2}}$,
综上可得$\frac{1+x}{1-x}$≤f(x)≤$\frac{1}{(1-x)^{2}}$;
(Ⅱ)解:由(Ⅰ)可知1+x≤e2x(1-x)≤$\frac{1}{1-x}$,
设m(x)=f(x)-g(x)=$\frac{1}{1-x}$[e2x(1-x)-(x2-ax-2xsinx+1)]
≥$\frac{1}{1-x}$(1+x-x2+ax+2xsinx-1)=$\frac{x}{1-x}$(1+a-x+2sinx),
令l(x)=-x+2sinx,则l′(x)=-1+2cosx>0,
∴函数l(x)在x∈[-1,0]上是增函数,.
∴l(x)≤l(0)=0,即1+a≤0,
可得a≤-1时,f(x)≥g(x)恒成立,
下面证明当a>-1时,f(x)≥g(x)不恒成立,
m(x)=f(x)-g(x)=$\frac{1}{1-x}$[e2x(1-x)-(x2-ax-2xsinx+1)]
≤$\frac{1}{1-x}$($\frac{1}{1-x}$+ax+2xsinx-1)=$\frac{x}{1-x}$($\frac{1}{1-x}$+a-x+2sinx),
令n(x)=$\frac{1}{1-x}$+a-x+2sinx,则n′(x)=$\frac{1}{(1-x)^{2}}$+l′(x)>0,
∴函数n(x)在x∈[-1,0]上是增函数,
∴函数n(x)在x∈[-1,0]上的值域为[$\frac{3}{2}+a-2sin1$,1+a],
∴存在x0∈[-1,0]使得n(x0)>0,m(x0)<0,
即f(x)≥g(x)不恒成立,
综上可得实数a取值范围为(-∞,-1]
点评 本题考查导数的综合应用,涉及导数法判函数的单调性,以及不等式的性质,属难题.

①方程f(x)=0至少有一个实数根;
②方程f(x)=0至多有两个实数根;
③函数f(x)的图象关于点(0,c)对称;
④当b≥0时,f(x)在R上是增函数.
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①③④ |

| A. | $\overrightarrow{AE}$•$\overrightarrow{FC}$=0 | B. | $\overrightarrow{AE}$•$\overrightarrow{DF}$>0 | C. | $\overrightarrow{FC}$=$\overrightarrow{FD}$+$\overrightarrow{FB}$ | D. | $\overrightarrow{FD}$•$\overrightarrow{FB}$<0 |
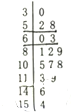 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)在15天内任取2天,求甲市空气质量类别均为良的概率;
(Ⅱ)在15天内任取2天,记甲市空气质量级别不超过三级的天数为X,求随机变量X的分布列及数学期望.

| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 6 |
| A. | $\frac{3}{2}$ | B. | 4 | C. | $\frac{5}{2}$ | D. | 2 |
 在如图所示的几何体中,四边形CDPQ为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面CDPQ⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.
在如图所示的几何体中,四边形CDPQ为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面CDPQ⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.