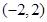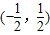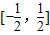题目内容
对任意的实数m,直线y=mx+b与椭圆x2+4y2=1恒有公共点,则b的取值范围是( )
分析:由直线y=mx+b与椭圆x2+4y2=1恒有公共点,知由其联立方程组恒有解,消掉y得关于x的二次方程,由△≥0对任意m恒成立可得b的范围.
解答:解:由
,得(1+4m2)x2+8mbx+4b2-1=0,
因为直线y=mx+b与椭圆x2+4y2=1恒有公共点,
所以△=64m2b2-(1+4m2)(4b2-1)≥0,即4b2≤4m2+1对任意m恒成立,
所以4b2≤1,解得-
≤b≤
,
故选B.
|
因为直线y=mx+b与椭圆x2+4y2=1恒有公共点,
所以△=64m2b2-(1+4m2)(4b2-1)≥0,即4b2≤4m2+1对任意m恒成立,
所以4b2≤1,解得-
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查直线与圆锥曲线的位置关系,考查函数恒成立问题,考查学生解决问题的能力.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
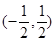 B.
B.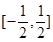 C.
C.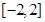 D.
D.