题目内容
已知对任意的实数m,直线x+y+m=0都不与曲线f(x)=x3-3ax(a∈R)相切.(I)求实数a的取值范围;
(II)当x∈[-1,1]时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于
| 1 | 4 |
分析:(I)由直线x+y+m=0得直线斜率为-1,直线x+y+m=0不与曲线f(x)相切知曲线f(x)上任一点斜率都不为-1,即f′(x)≠-1,求导函数,并求出其范围[-3a,+∞),得不等式-3a>-1,得实数a的取值范围;
(II)转化问题,等价于当x∈[-1,1]时,|f(x)|max≥
,设g(x)=|f(x)|,观察出g(x)在[-1,1]上是偶函数,只需求g(x)在[0,1]上的最大值,求函数单调性时,因为含有参数,所以要对参数进行讨论,分为两类求解,在每一类都可证明g(x)max≥
,问题得证.
(II)转化问题,等价于当x∈[-1,1]时,|f(x)|max≥
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(I)f′(x)=3x2-3a∈[-3a,+∞),
∵对任意的实数m,直线x+y+m=0都不与曲线f(x)=x3-3ax(a∈R)相切,
∴-1∉[-3a,+∞),∴-3a>-1,∴实数a的取值范围为a<
;
(II)存在,证明:问题等价于当x∈[-1,1]时,|f(x)|max≥
,
设g(x)=|f(x)|,则g(x)在[-1,1]上是偶函数,
故只要证明当x∈[0,1]时,|f(x)|max≥
,
①当a≤0时,f′(x)=3x2-3a≥0,f(x)在[0,1]上单调递增,且f(0)=0,g(x)=f(x),
g(x)max=f(1)=1-3a>1>
;
②当0<a<
时,f′(x)=3x2-3a=3(x+
)(x-
),
令f′(x)<0,得0<x<
,令f′(x)>0得
<x<1,
∴f(x)在[0,
]上单调递减,在[
,1]上单调递增,
注意到f(0)=f(
)=0,且
<
<1,
∴x∈(0,
)时,g(x)=-f(x),x∈(
,1]时,g(x)=f(x),
∴g(x)max=max{f(1),-f(
)},
由f(1)=1-3a≥
及0<a<
,解得0<a≤
,此时-f(
)≤f(1)成立.
∴g(x)max=f(1)=1-3a≥
.
由-f(
)=2a
≥
及0<a<
,解得
≤a<
,此时-f(
)≥f(1)成立.
∴g(x)max=-f(
)=2a
≥
.
∴在x∈[-1,1]上至少存在一个x0,使得|f(x0)|≥
成立,
即当x∈[-1,1]时,函数y=f(x)的图象上至少存在一点P,使得点P到x轴的距离不小于
.
∵对任意的实数m,直线x+y+m=0都不与曲线f(x)=x3-3ax(a∈R)相切,
∴-1∉[-3a,+∞),∴-3a>-1,∴实数a的取值范围为a<
| 1 |
| 3 |
(II)存在,证明:问题等价于当x∈[-1,1]时,|f(x)|max≥
| 1 |
| 4 |
设g(x)=|f(x)|,则g(x)在[-1,1]上是偶函数,
故只要证明当x∈[0,1]时,|f(x)|max≥
| 1 |
| 4 |
①当a≤0时,f′(x)=3x2-3a≥0,f(x)在[0,1]上单调递增,且f(0)=0,g(x)=f(x),
g(x)max=f(1)=1-3a>1>
| 1 |
| 4 |
②当0<a<
| 1 |
| 3 |
| a |
| a |
令f′(x)<0,得0<x<
| a |
| a |
∴f(x)在[0,
| a |
| a |
注意到f(0)=f(
| 3a |
| a |
| 3a |
∴x∈(0,
| 3a |
| 3a |
∴g(x)max=max{f(1),-f(
| a |
由f(1)=1-3a≥
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| a |
∴g(x)max=f(1)=1-3a≥
| 1 |
| 4 |
由-f(
| a |
| a |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| a |
∴g(x)max=-f(
| a |
| a |
| 1 |
| 4 |
∴在x∈[-1,1]上至少存在一个x0,使得|f(x0)|≥
| 1 |
| 4 |
即当x∈[-1,1]时,函数y=f(x)的图象上至少存在一点P,使得点P到x轴的距离不小于
| 1 |
| 4 |
点评:本题考查导数在最大值,最小值问题中的应用,难点之一为利用导数求函数单调性时,式子里面有参数,要对参数进行分类讨论,难点之二要清楚原函数f(x)的零点,排除f(0)为最大值的可能,同时得出g(x)与f(x)的关系.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
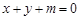 都不与曲线
都不与曲线 相切.
相切. 的取值范围;
的取值范围; 时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于
时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于 .试证明你的结论.
.试证明你的结论. .试证明你的结论.
.试证明你的结论.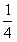 ,试证明你的结论。
,试证明你的结论。