题目内容
已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【命题意图】本题考查导数的应用,分类讨论思想,考查运算求解能力、逻辑思维能力和分析问题解决问题的能力,中等题.
【答案】(Ⅰ)当a=1时,f(x)=x2-3x+lnx,定义域为(0,+∞).
f′(x)=2x-3+![]() =
=![]() =
=![]() .
.
令f′(x)=0,得x=1,或x=![]() .…………………………………………………………………3分
.…………………………………………………………………3分
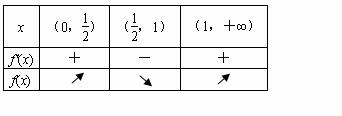
所以函数f(x)的单调增区间为(0,![]() )和(1,+∞).…………………………………………6分
)和(1,+∞).…………………………………………6分
(Ⅱ)f′(x)=2x-(2a+1)+![]() =
=![]() =
=![]() .
.
令f′(x)=0,得x=a,或x=![]() . …………………………………………………………^……7分
. …………………………………………………………^……7分
当a≤1时,不论![]() 还是
还是![]() ,在区间
,在区间![]() 上,
上,![]() 均为增函数。
均为增函数。
所以[f(x)]min=f(1) =-2a;…………………………………………………………………………8分
当1<a<e时,

所以[f(x)]min=f(a) =a(lna-a-1);…………………………………………………………………10分
当a≥e时,
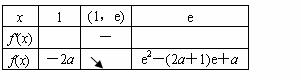
所以[f(x)]min=f(e) =e2-(2a+1) e+a.……………………………………………………………12分
综上,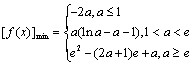 . ……………………………13分
. ……………………………13分

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目