题目内容
已知函数 .
.(1)当m=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当m=1时,证明方程f(x)=g(x)有且仅有一个实数根;
(3)若x∈(1,e]时,不等式f(x)-g(x)<2恒成立,求实数m的取值范围.
【答案】分析:(1)m=2时,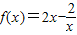 ,求出导函数f'(x),从而求出f'(1)得到切线的斜率,求出切点,根据点斜式可求出切线方程;
,求出导函数f'(x),从而求出f'(1)得到切线的斜率,求出切点,根据点斜式可求出切线方程;
(2)m=1时,令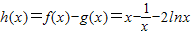 ,求出h'(x),判定符号得到函数在(0,+∞)上的单调性,然后判定
,求出h'(x),判定符号得到函数在(0,+∞)上的单调性,然后判定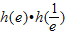 的符号,根据根的存在性定理可得结论;
的符号,根据根的存在性定理可得结论;
(3)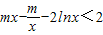 恒成立,即m(x2-1)<2x+2xlnx恒成立,讨论x2-1的符号将m分离出来,利用导数研究不等式另一侧的最值,从而求出m的取值范围.
恒成立,即m(x2-1)<2x+2xlnx恒成立,讨论x2-1的符号将m分离出来,利用导数研究不等式另一侧的最值,从而求出m的取值范围.
解答:解:(1)m=2时,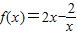 ,
,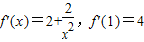 ,
,
切点坐标为(1,0),
∴切线方程为y=4x-4…(2分)
(2)m=1时,令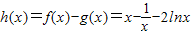 ,
,
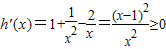 ,
,
∴h(x)在(0,+∞)上为增函数.…(4分)
又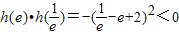 ,
,
∴y=h(x)在(0,+∞)内有且仅有一个零点
∴在(0,+∞)内f(x)=g(x)有且仅有一个实数根 …(6分)
(或说明h(1)=0也可以)
(3)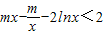 恒成立,即m(x2-1)<2x+2xlnx恒成立,
恒成立,即m(x2-1)<2x+2xlnx恒成立,
又x2-1>0,则当x∈(1,e]时,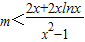 恒成立,
恒成立,
令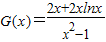 ,只需m小于G(x)的最小值,
,只需m小于G(x)的最小值,
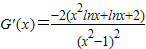 ,
,
∵1<x≤e,∴lnx>0,∴当x∈(1,e]时G'(x)<0,
∴G(x)在(1,e]上单调递减,
∴G(x)在(1,e]的最小值为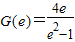 ,
,
则m的取值范围是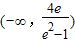 . …(12分)
. …(12分)
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及根的存在性和利用导数求闭区间上函数的最值,同时考查了分类讨论的数学思想,属于中档题.
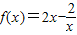 ,求出导函数f'(x),从而求出f'(1)得到切线的斜率,求出切点,根据点斜式可求出切线方程;
,求出导函数f'(x),从而求出f'(1)得到切线的斜率,求出切点,根据点斜式可求出切线方程;(2)m=1时,令
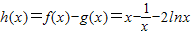 ,求出h'(x),判定符号得到函数在(0,+∞)上的单调性,然后判定
,求出h'(x),判定符号得到函数在(0,+∞)上的单调性,然后判定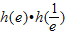 的符号,根据根的存在性定理可得结论;
的符号,根据根的存在性定理可得结论;(3)
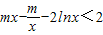 恒成立,即m(x2-1)<2x+2xlnx恒成立,讨论x2-1的符号将m分离出来,利用导数研究不等式另一侧的最值,从而求出m的取值范围.
恒成立,即m(x2-1)<2x+2xlnx恒成立,讨论x2-1的符号将m分离出来,利用导数研究不等式另一侧的最值,从而求出m的取值范围.解答:解:(1)m=2时,
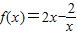 ,
,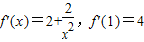 ,
,切点坐标为(1,0),
∴切线方程为y=4x-4…(2分)
(2)m=1时,令
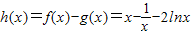 ,
,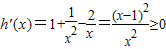 ,
,∴h(x)在(0,+∞)上为增函数.…(4分)
又
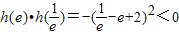 ,
,∴y=h(x)在(0,+∞)内有且仅有一个零点
∴在(0,+∞)内f(x)=g(x)有且仅有一个实数根 …(6分)
(或说明h(1)=0也可以)
(3)
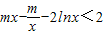 恒成立,即m(x2-1)<2x+2xlnx恒成立,
恒成立,即m(x2-1)<2x+2xlnx恒成立,又x2-1>0,则当x∈(1,e]时,
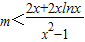 恒成立,
恒成立,令
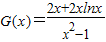 ,只需m小于G(x)的最小值,
,只需m小于G(x)的最小值,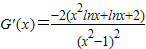 ,
,∵1<x≤e,∴lnx>0,∴当x∈(1,e]时G'(x)<0,
∴G(x)在(1,e]上单调递减,
∴G(x)在(1,e]的最小值为
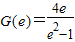 ,
,则m的取值范围是
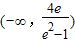 . …(12分)
. …(12分)点评:本题主要考查了利用导数研究曲线上某点切线方程,以及根的存在性和利用导数求闭区间上函数的最值,同时考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 .
. 上的取值范围;
上的取值范围; ,求m的值.
,求m的值. .
. 上的取值范围;
上的取值范围; ,求m的值.
,求m的值.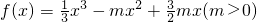 .
.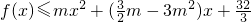 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.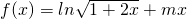 .
. .
.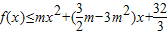 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.