题目内容
已知函数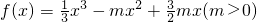 .
.
(1)当m=2时,求曲线y=f(x)在点(0,0)处的切线方程;
(2)讨论函数y=f(x)的单调性;
(3)若函数f(x)既有极大值,又有极小值,且当0≤x≤4m时,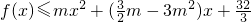 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
解:(1)m=2时,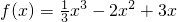 ,
,
f′(x)=x2-4x+3,
函数在(0,0)处切线的斜率为f′(0)=3,
∴在(0,0)处切线方程为:3x-y=0.
(2)函数f(x)的定义域为R,
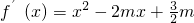 ,
,
方程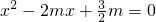 的判别式△=4m2-6m,
的判别式△=4m2-6m,
①当△=4m2-6m≤0,即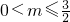 时,f′(x)≥0对一切实数恒成立,
时,f′(x)≥0对一切实数恒成立,
∴f(x)在(-∞,+∞)上单调递增;
②当△=4m2-6m>0,即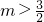 时,
时,
方程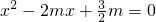 有两不等实根,
有两不等实根,
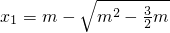 ,
, ,
,
当x∈(-∞,x1)及(x2,+∞)时,
f′(x)>0,∴f(x)单调递增;
当x∈(x1,x2)时,
f′(x)<0,∴f(x)单调递减.
综上所述,当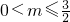 时,
时,
f(x)在(-∞,+∞)上单调递增;
当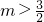 时,f(x)在
时,f(x)在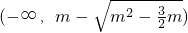 及
及 上单调递增,
上单调递增,
在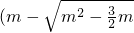 ,
,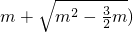 上单调递减.
上单调递减.
(3)由(2)知方程 有两不等根,
有两不等根,
△=4m2-6m>0,即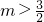 ,
,
令g(x)=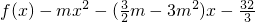 =
=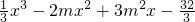 ,
,
要使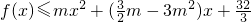 对0≤x≤4m的实数恒成立,
对0≤x≤4m的实数恒成立,
只需g(x)max≤0即可,
下面求g(x)在x∈[0,4m]上的最大值,
∵g′(x)=x2-4mx+3m2,令g′(x)=(x-m)(x-3m)=0,
则x=m,x=3m, ,
,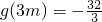 ,
,
又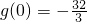 ,
,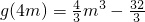 ,
,
∴当x∈[0,4m]时,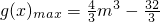 ,
,
∴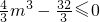 ,
,
即m≤2,又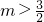 ,
,
∴m的取值范围为 .
.
分析:(1)m=2时,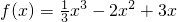 ,f′(x)=x2-4x+3,由此能求出函数在(0,0)处切线方程.
,f′(x)=x2-4x+3,由此能求出函数在(0,0)处切线方程.
(2)函数f(x)的定义域为R,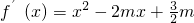 ,方程
,方程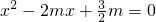 的判别式△=4m2-6m,由此入手能够分类讨论函数y=f(x)的单调性.
的判别式△=4m2-6m,由此入手能够分类讨论函数y=f(x)的单调性.
(3)由 有两不等根,△=4m2-6m>0,即
有两不等根,△=4m2-6m>0,即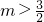 ,令g(x)=
,令g(x)=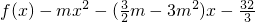 =
=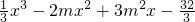 ,由此能求出m的取值范围.
,由此能求出m的取值范围.
点评:本题考查曲线的切线方程的求法,考查函数的单调性的求法,考查实数的取值范围的求法,考查导数的性质及其应用.解题时要认真审题,仔细解答,注意分类讨论思想和等价转化思想的应用.
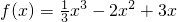 ,
,f′(x)=x2-4x+3,
函数在(0,0)处切线的斜率为f′(0)=3,
∴在(0,0)处切线方程为:3x-y=0.
(2)函数f(x)的定义域为R,
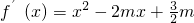 ,
,方程
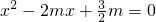 的判别式△=4m2-6m,
的判别式△=4m2-6m,①当△=4m2-6m≤0,即
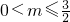 时,f′(x)≥0对一切实数恒成立,
时,f′(x)≥0对一切实数恒成立,∴f(x)在(-∞,+∞)上单调递增;
②当△=4m2-6m>0,即
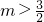 时,
时,方程
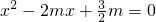 有两不等实根,
有两不等实根,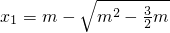 ,
, ,
,当x∈(-∞,x1)及(x2,+∞)时,
f′(x)>0,∴f(x)单调递增;
当x∈(x1,x2)时,
f′(x)<0,∴f(x)单调递减.
综上所述,当
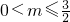 时,
时,f(x)在(-∞,+∞)上单调递增;
当
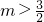 时,f(x)在
时,f(x)在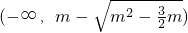 及
及 上单调递增,
上单调递增,在
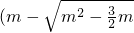 ,
,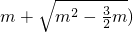 上单调递减.
上单调递减.(3)由(2)知方程
 有两不等根,
有两不等根,△=4m2-6m>0,即
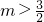 ,
,令g(x)=
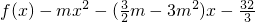 =
=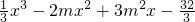 ,
,要使
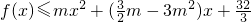 对0≤x≤4m的实数恒成立,
对0≤x≤4m的实数恒成立,只需g(x)max≤0即可,
下面求g(x)在x∈[0,4m]上的最大值,
∵g′(x)=x2-4mx+3m2,令g′(x)=(x-m)(x-3m)=0,
则x=m,x=3m,
 ,
,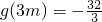 ,
,又
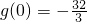 ,
,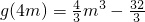 ,
,∴当x∈[0,4m]时,
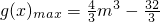 ,
,∴
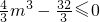 ,
,即m≤2,又
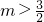 ,
,∴m的取值范围为
 .
.分析:(1)m=2时,
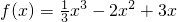 ,f′(x)=x2-4x+3,由此能求出函数在(0,0)处切线方程.
,f′(x)=x2-4x+3,由此能求出函数在(0,0)处切线方程.(2)函数f(x)的定义域为R,
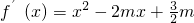 ,方程
,方程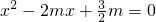 的判别式△=4m2-6m,由此入手能够分类讨论函数y=f(x)的单调性.
的判别式△=4m2-6m,由此入手能够分类讨论函数y=f(x)的单调性.(3)由
 有两不等根,△=4m2-6m>0,即
有两不等根,△=4m2-6m>0,即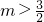 ,令g(x)=
,令g(x)=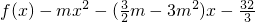 =
=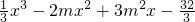 ,由此能求出m的取值范围.
,由此能求出m的取值范围.点评:本题考查曲线的切线方程的求法,考查函数的单调性的求法,考查实数的取值范围的求法,考查导数的性质及其应用.解题时要认真审题,仔细解答,注意分类讨论思想和等价转化思想的应用.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 .
. 上的取值范围;
上的取值范围; ,求m的值.
,求m的值. .
. 上的取值范围;
上的取值范围; ,求m的值.
,求m的值.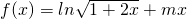 .
. .
.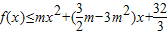 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.