题目内容
已知{an}是等比数列,a2=2,a5=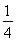 ,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
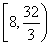
【解析】∵a5=a2q3,∴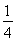 =2×q3,∴q=
=2×q3,∴q=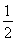 ,∴a1=
,∴a1=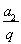 =4,∴an=4×
=4,∴an=4×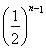 =23-n,
=23-n,
∴akak+1=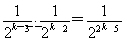 ,∴a1a2+a2a3+…+anan+1=
,∴a1a2+a2a3+…+anan+1=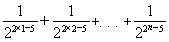
=32×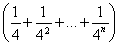 =32×
=32×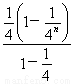 =
=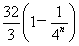 ∈
∈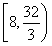 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知{an}是等比数列,a2=2,a5=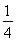 ,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
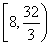
【解析】∵a5=a2q3,∴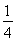 =2×q3,∴q=
=2×q3,∴q=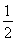 ,∴a1=
,∴a1=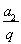 =4,∴an=4×
=4,∴an=4×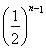 =23-n,
=23-n,
∴akak+1=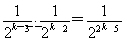 ,∴a1a2+a2a3+…+anan+1=
,∴a1a2+a2a3+…+anan+1=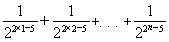
=32×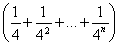 =32×
=32×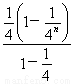 =
=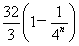 ∈
∈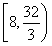 .
.

 阅读快车系列答案
阅读快车系列答案