题目内容
12.已知cosπx≤$\frac{1}{2}$,则x的取值范围是[2k+$\frac{1}{3}$,2k+$\frac{5}{3}$],k∈Z.分析 根据余弦函数的性质,解不等式即可.
解答 解:由cosπx≤$\frac{1}{2}$,
得$\frac{π}{3}$+2kπ≤πx≤2kπ+$\frac{5π}{3}$,k∈Z,
即2k+$\frac{1}{3}$≤x≤2k+$\frac{5}{3}$,k∈Z,
故答案为:[2k+$\frac{1}{3}$,2k+$\frac{5}{3}$],k∈Z
点评 本题主要考查余弦函数的求解,比较基础.

练习册系列答案
相关题目
3.设函数f(x)=$\frac{2}{x}$+lnx则( )
| A. | x=2为f(x)的极小值点 | B. | x=2为f(x)的极大值点 | ||
| C. | $x=\frac{1}{2}$为f(x)的极小值点 | D. | $x=\frac{1}{2}$为f(x)的极大值点 |
 的连续可导函数
的连续可导函数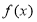 ,若满足以下两个条件:
,若满足以下两个条件: 没有零点,
没有零点,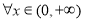 ,都有
,都有 .
. 方程
方程 有( )个解.
有( )个解. 的夹角为60°,则
的夹角为60°,则 在
在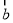 方向上的投影为 ;
方向上的投影为 ;