题目内容
1.在锐角△ABC中,角A,B,C的对边分别为a,b,c,且$bcosC=\sqrt{2}acosB-ccosB$,(1)求角B的值;
(2)设A=θ,求函数$f(θ)=2{sin^2}({\frac{π}{4}+θ})-\sqrt{3}cos2θ$的取值范围.
分析 (1)由正弦定理化简已知得sin(B+C)=$\sqrt{2}$sinAcosB,从而可求cosB,即可求得B.
(2)由(1)可求θ∈($\frac{π}{4}$,$\frac{π}{2}$),利用三角函数恒等变换的应用化简可得f(θ)=2sin(2θ-$\frac{π}{3}$)+1,由2θ-$\frac{π}{3}$∈($\frac{π}{6}$,$\frac{2π}{3}$),利用正弦函数的性质即可求得取值范围.
解答 (本小题满分12分)
解:(1)∵由正弦定理得a=2RsinA,b=2RsinB,c=2RsinC,sin(B+C)=$\sqrt{2}$sinAcosB,
∴cosB=$\frac{\sqrt{2}}{2}$,
∴B=$\frac{π}{4}$.…(6分)
(2)锐角△ABC中,A+B=$\frac{3π}{4}$,∴θ∈($\frac{π}{4}$,$\frac{π}{2}$),…(7分)
$f(θ)=2{sin^2}({\frac{π}{4}+θ})-\sqrt{3}cos2θ$=[1-cos($\frac{π}{2}$+2θ)]-$\sqrt{3}$cos2θ
=(1+sin2θ)-$\sqrt{3}$cos2θ
=sin2θ-$\sqrt{3}$cos2θ+1=2sin(2θ-$\frac{π}{3}$)+1.…9分
∵θ∈($\frac{π}{4}$,$\frac{π}{2}$),
∴2θ-$\frac{π}{3}$∈($\frac{π}{6}$,$\frac{2π}{3}$),
∴2<2sin(2θ-$\frac{π}{3}$)+1≤3.
所以:函数f(θ)的取值范围是(2,3].…12分
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,考查了正弦函数的图象和性质,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既不是奇函数也不是偶函数 | D. | 既是奇函数也是偶函数 |
| A. | (1,2) | B. | ($\frac{1}{10},1$) | C. | (2,3) | D. | (-∞,0) |
| A. | 2 | B. | 6 | C. | 2或6 | D. | 2或-6 |
 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: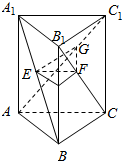 如图所示,在正三棱柱ABC-A1B1C1中,E,F,G是侧面对角线上的点,且BE=CF=AG,求证:平面EFG∥平面ABC.
如图所示,在正三棱柱ABC-A1B1C1中,E,F,G是侧面对角线上的点,且BE=CF=AG,求证:平面EFG∥平面ABC.