题目内容
已知a,b∈R,矩阵A=
所对应的变换TA将直线2x-y-3=0变换为自身.
(1)求实数a,b的值;
(2)计算A2
.
|
(1)求实数a,b的值;
(2)计算A2
|
分析:(1)首先分析题目已知A=
所对应的变换TA把直线:2x-y-3=0变换为自身,故可根据变换的性质列出一组方程式求解出a,b;
(2)由(1)即可得到矩阵M,再根据矩阵的乘法运算求出A2
即可.
|
(2)由(1)即可得到矩阵M,再根据矩阵的乘法运算求出A2
|
解答:解:(1)设直线2x-y-3=0上任意一点P(x,y)在变换TA的作用下变成点P'(x',y'),
由题意知2x'-y'-3=0,由
=
得x'=-x+ay,y'=bx+3y,…(2分)
代入直线2x'-y'-3=0得2(-x+ay)-(bx+3y)-3=0,
即(-b-2)x+(2a-3)y-3=0,
由点P(x,y)的任意性可得-b-2=2,2a-3=-1,
解得a=1,b=-4. …(5分)
(2)由(1)得A2=
=
,…(7分)
则A2
=
=
. …(10分)
由题意知2x'-y'-3=0,由
|
|
|
得x'=-x+ay,y'=bx+3y,…(2分)
代入直线2x'-y'-3=0得2(-x+ay)-(bx+3y)-3=0,
即(-b-2)x+(2a-3)y-3=0,
由点P(x,y)的任意性可得-b-2=2,2a-3=-1,
解得a=1,b=-4. …(5分)
(2)由(1)得A2=
|
|
|
则A2
|
|
|
|
点评:此题主要考查矩阵变换的问题,其中涉及到矩阵的乘法,题中是用一般方法求解,也可根据取特殊值法求解,具体题目具体分析找到最简便的方法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.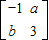 所对应的变换TA将直线2x-y-3=0变换为自身.
所对应的变换TA将直线2x-y-3=0变换为自身.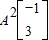 .
.