题目内容
已知空间向量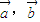 满足
满足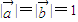 ,且
,且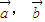 的夹角为
的夹角为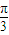 ,O为空间直角坐标系的原点,点A、B满足
,O为空间直角坐标系的原点,点A、B满足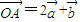 ,
,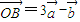 ,则△OAB的面积为( )
,则△OAB的面积为( )A.
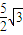
B.
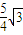
C.
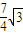
D.
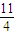
【答案】分析:由向量的运算可得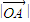 ,
,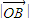 ,以及
,以及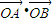 ,代入夹角公式可得cos∠BOA,由平方关系可得sin∠BOA,代入三角形的面积公式S=
,代入夹角公式可得cos∠BOA,由平方关系可得sin∠BOA,代入三角形的面积公式S=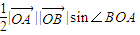 ,计算可得.
,计算可得.
解答:解:由题意可得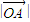 =
=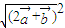 =
=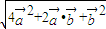 =
=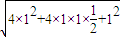 =
=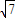 ,
,
同理可得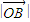 =
=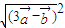 =
=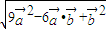 =
=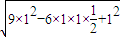 =
=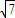 ,
,
而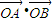 =(
=( )•(
)•(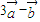 )=
)=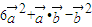 =6×12
=6×12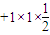 -12=
-12=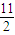 ,
,
故cos∠BOA=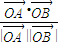 =
=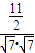 =
=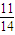 ,可得sin∠BOA=
,可得sin∠BOA=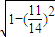 =
=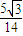 ,
,
所以△OAB的面积S=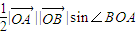 =
=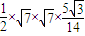 =
=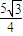 .
.
故选B
点评:本题考查平面向量的数量积和三角形面积的求解,熟练掌握公式是解决问题的关键,属中档题.
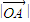 ,
,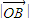 ,以及
,以及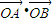 ,代入夹角公式可得cos∠BOA,由平方关系可得sin∠BOA,代入三角形的面积公式S=
,代入夹角公式可得cos∠BOA,由平方关系可得sin∠BOA,代入三角形的面积公式S=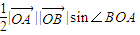 ,计算可得.
,计算可得.解答:解:由题意可得
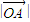 =
=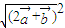 =
=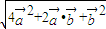 =
=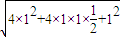 =
=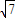 ,
,同理可得
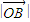 =
=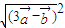 =
=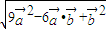 =
=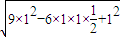 =
=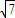 ,
,而
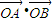 =(
=( )•(
)•(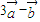 )=
)=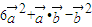 =6×12
=6×12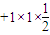 -12=
-12=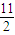 ,
,故cos∠BOA=
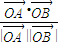 =
=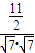 =
=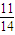 ,可得sin∠BOA=
,可得sin∠BOA=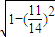 =
=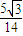 ,
,所以△OAB的面积S=
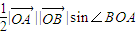 =
=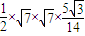 =
=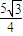 .
.故选B
点评:本题考查平面向量的数量积和三角形面积的求解,熟练掌握公式是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知空间向量
,
满足条件:(
+3
)⊥(7
-5
),且(
-4
)⊥(7
-2
),则空间向量
,
的夹角<
,
>( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、等于30° | B、等于45° |
| C、等于60° | D、不确定 |
 ,
,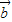 满足条件:(
满足条件:(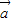 +3
+3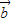 )⊥(7
)⊥(7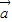 -5
-5 ),且(
),且(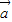 -4
-4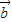 )⊥(7
)⊥(7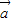 -2
-2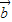 ),则空间向量
),则空间向量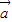 ,
,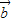 的夹角<
的夹角<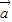 ,
,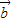 >( )
>( )