题目内容
 在如图的1×6矩形长条中涂上红、黄、蓝三种颜色,每种颜色限涂两格,且相邻两格不同色,则不同的涂色方案有
在如图的1×6矩形长条中涂上红、黄、蓝三种颜色,每种颜色限涂两格,且相邻两格不同色,则不同的涂色方案有30
30
种.分析:本题是有条件限制排列问题,先给左边第一个位置涂色,可以涂3种不同的颜色中的任意一种,再给第二个位置涂色,只能涂剩余的两种中的一种,第三个位置上的颜色可以与第一个位置上相同,相同时后三个位置只有一种涂法,也可以不同,不同时也不能与第二个位置上的颜色相同,此时第四个位置上的颜色要么与第一个位置上的颜色相同,要么与第二个位置上的颜色相同,不论是那种情况五、六位置上都还有两种涂法.
解答:解:先给左边第一个位置涂色,可以涂3种不同的颜色中的任意一种,有
=3种涂法,再给第二个位置涂色,只能涂剩余的两种中的一种有
=2种涂法,第三个位置上的颜色与第一个位置上相同只有1种涂法,第三个位置上的颜色与第一个位置上不同有2×2=4种涂法,所以总的不同的涂色方案有3×2×(1+2×2)=30种.
故答案为30.
| C | 1 3 |
| C | 1 2 |
故答案为30.
点评:本题考查了排列、组合及简单的计数问题,解答此题的关键是正确分类,分类要做到不重不漏,是中等难度的计算题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
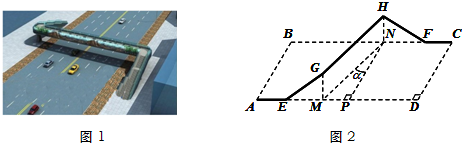
 如图所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、BA的方向运动,当第二次MF=MN时M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,设动点M、N的速度都是1个单位/秒,M、N运动的时间为t秒.试解答下列问题:
如图所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2.动点M、N分别从点D、B同时出发,沿射线DA、BA的方向运动,当第二次MF=MN时M、N两点同时停止运动.连接FM、FN,当F、N、M不在同一直线时,可得△FMN,设动点M、N的速度都是1个单位/秒,M、N运动的时间为t秒.试解答下列问题: (2013•淄博一模)在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
(2013•淄博一模)在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点. (2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(
(2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(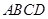 的三边
的三边 、
、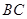 、
、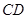 由长6分米的材料弯折而成,
由长6分米的材料弯折而成,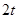 分米(
分米(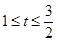 );曲线
);曲线 拟从以下两种曲线中选择一种:曲线
拟从以下两种曲线中选择一种:曲线 是一段余弦曲线
是一段余弦曲线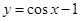 ),此时记门的最高点
),此时记门的最高点 到
到 ;曲线
;曲线 是一段抛物线,其焦点到准线的距离为
是一段抛物线,其焦点到准线的距离为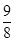 ,此时记门的最高点
,此时记门的最高点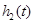 .
.