题目内容
甲、乙二射击运动员分别对一目标射击 次,甲射中的概率为
次,甲射中的概率为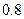 ,乙射中的概率为
,乙射中的概率为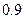 ,求:
,求:
(1)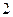 人都射中目标的概率;
人都射中目标的概率;
(2)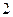 人中恰有
人中恰有 人射中目标的概率;
人射中目标的概率;
(3)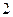 人至少有
人至少有 人射中目标的概率;
人射中目标的概率;
(4)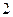 人至多有
人至多有 人射中目标的概率?
人射中目标的概率?
 次,甲射中的概率为
次,甲射中的概率为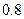 ,乙射中的概率为
,乙射中的概率为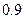 ,求:
,求:(1)
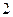 人都射中目标的概率;
人都射中目标的概率;(2)
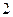 人中恰有
人中恰有 人射中目标的概率;
人射中目标的概率;(3)
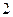 人至少有
人至少有 人射中目标的概率;
人射中目标的概率;(4)
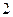 人至多有
人至多有 人射中目标的概率?
人射中目标的概率?(1)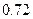 (2)
(2)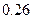 (3)
(3)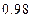 (4)
(4)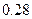
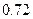 (2)
(2)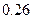 (3)
(3)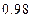 (4)
(4)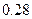
记“甲射击 次,击中目标”为事件
次,击中目标”为事件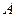 ,“乙射击
,“乙射击 次,击中目标”为事件
次,击中目标”为事件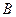 ,则
,则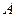 与
与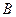 ,
,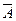 与
与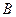 ,
,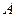 与
与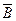 ,
,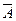 与
与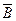 为相互独立事件,
为相互独立事件,
(1)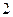 人都射中的概率为:
人都射中的概率为:
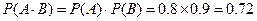 ,
,
∴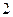 人都射中目标的概率是
人都射中目标的概率是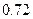 .
.
(2)“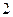 人各射击
人各射击 次,恰有
次,恰有 人射中目标”包括两种情况:一种是甲击中、乙未击中(事件
人射中目标”包括两种情况:一种是甲击中、乙未击中(事件 发生),另一种是甲未击中、乙击中(事件
发生),另一种是甲未击中、乙击中(事件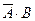 发生)
发生) 根据题意,事件
根据题意,事件 与
与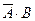 互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为:
互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为:
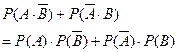
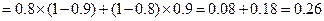
∴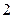 人中恰有
人中恰有 人射中目标的概率是
人射中目标的概率是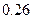 .
.
(3)(法1):2人至少有1人射中包括“2人都中”和“2人有1人不中”2种情况,其概率为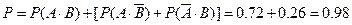 .
.
(法2):“2人至少有一个击中”与“2人都未击中”为对立事件,
2个都未击中目标的概率是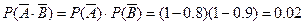 ,
,
∴“两人至少有1人击中目标”的概率为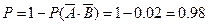 .
.
(4)(法1):“至多有1人击中目标”包括“有1人击中”和“2人都未击中”,
故所求概率为:
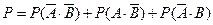
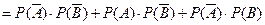
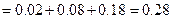 .
.
(法2):“至多有1人击中目标”的对立事件是“2人都击中目标”,
故所求概率为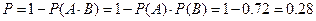

 次,击中目标”为事件
次,击中目标”为事件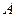 ,“乙射击
,“乙射击 次,击中目标”为事件
次,击中目标”为事件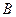 ,则
,则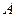 与
与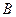 ,
,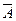 与
与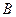 ,
,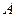 与
与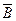 ,
,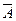 与
与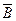 为相互独立事件,
为相互独立事件,(1)
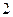 人都射中的概率为:
人都射中的概率为: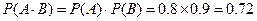 ,
,∴
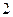 人都射中目标的概率是
人都射中目标的概率是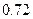 .
.(2)“
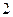 人各射击
人各射击 次,恰有
次,恰有 人射中目标”包括两种情况:一种是甲击中、乙未击中(事件
人射中目标”包括两种情况:一种是甲击中、乙未击中(事件 发生),另一种是甲未击中、乙击中(事件
发生),另一种是甲未击中、乙击中(事件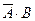 发生)
发生) 根据题意,事件
根据题意,事件 与
与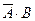 互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为:
互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为: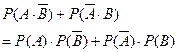
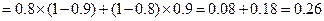
∴
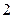 人中恰有
人中恰有 人射中目标的概率是
人射中目标的概率是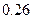 .
.(3)(法1):2人至少有1人射中包括“2人都中”和“2人有1人不中”2种情况,其概率为
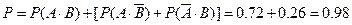 .
.(法2):“2人至少有一个击中”与“2人都未击中”为对立事件,
2个都未击中目标的概率是
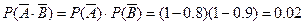 ,
,∴“两人至少有1人击中目标”的概率为
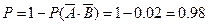 .
.(4)(法1):“至多有1人击中目标”包括“有1人击中”和“2人都未击中”,
故所求概率为:
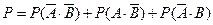
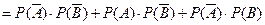
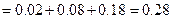 .
.(法2):“至多有1人击中目标”的对立事件是“2人都击中目标”,
故所求概率为
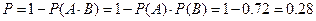


练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
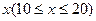 万件的该种产品所需要的总成本为
万件的该种产品所需要的总成本为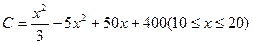 万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.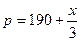
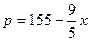
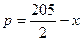
 个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这
个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这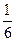

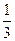
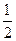
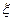 的数学期望.
的数学期望.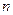 次重复试验得
次重复试验得 到某个事件
到某个事件 发生的频率
发生的频率 ,则随着
,则随着