题目内容
 A.不等式
A.不等式| x-2 |
| x2+3x+2 |
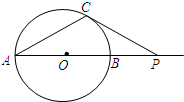
B.如图,AB是⊙O的直径,P是AB延长线上的一点,过P作⊙O的切线,切点为CPC=2
| 3 |
C.(极坐标系与参数方程选做题)若圆C:
|
分析:A、根据实数的性质,将问题转化为一个一元高次不等式,用标根法,易求出答案.
B、由AB是⊙O的直径,P是AB延长线上的一点,过P作⊙O的切线,切点为CPC=2
,若∠CAP=30°,我们可判断出△OPC是以∠OCP为直角,∠P=30°的直角三角形,求出圆的半径后,进而求出圆的直径.
C、由圆的参数方程,我们可以求出圆的标准方程,根据圆与直线相切,圆心到直线的距离等于半径,结合点到直线距离公式,构造关于m的方程,解方程即可得到答案.
B、由AB是⊙O的直径,P是AB延长线上的一点,过P作⊙O的切线,切点为CPC=2
| 3 |
C、由圆的参数方程,我们可以求出圆的标准方程,根据圆与直线相切,圆心到直线的距离等于半径,结合点到直线距离公式,构造关于m的方程,解方程即可得到答案.
解答:解:A、不等式
>0可化为:
(x+2)(x+1)(x-2)>0
解得:-2<x<-1或x>2
故答案为:(-2,-1)∪(2,+∞)
B、∵AB是⊙O的直径,∠CAP=30°,
∴△OPC是以∠OCP为直角,∠P=30°的直角三角形
又∵PC=2
∴圆的半径OC=2
故圆的直径为4
故答案为4
C、由圆C:
(θ为参数)
我们易求出圆的标准方程为:
(x-1)2+(y-2)2=2
又∵圆C与直线x-y+m=0相切
∴圆心(1,2)直线的距离d等于半径r
即d=
=
解得m=3或-1
故答案为:3或-1
| x-2 |
| x2+3x+2 |
(x+2)(x+1)(x-2)>0
解得:-2<x<-1或x>2
故答案为:(-2,-1)∪(2,+∞)
B、∵AB是⊙O的直径,∠CAP=30°,
∴△OPC是以∠OCP为直角,∠P=30°的直角三角形
又∵PC=2
| 3 |
∴圆的半径OC=2
故圆的直径为4
故答案为4
C、由圆C:
|
我们易求出圆的标准方程为:
(x-1)2+(y-2)2=2
又∵圆C与直线x-y+m=0相切
∴圆心(1,2)直线的距离d等于半径r
即d=
| |1-2+m| | ||
|
| 2 |
解得m=3或-1
故答案为:3或-1
点评:本题考查的知识点是分式方程的解法,圆的切线的性质定理,直线与圆的位置关系,A中关键是要将不等式转化为整式不等式,B中关键是判断出△OPC是以∠OCP为直角,∠P=30°的直角三角形,C中关键是求出圆的标准方程.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
不等式
<0的解集为( )
| x-2 |
| x2- 1 |
| A、{x|1<x<2} |
| B、{x|x<2且x≠1} |
| C、{x|-1<x<2且x≠1} |
| D、{x|x<-1或1<x<2} |